Exam 13: Introduction to Optimization Modeling
Exam 1: Introduction to Business Analytics29 Questions
Exam 2: Describing the Distribution of a Single Variable100 Questions
Exam 3: Finding Relationships Among Variables85 Questions
Exam 4: Probability and Probability Distributions114 Questions
Exam 5: Normal, Binomial, Poisson, and Exponential Distributions125 Questions
Exam 6: Decision Making Under Uncertainty107 Questions
Exam 7: Sampling and Sampling Distributions90 Questions
Exam 8: Confidence Interval Estimation84 Questions
Exam 9: Hypothesis Testing87 Questions
Exam 10: Regression Analysis: Estimating Relationships92 Questions
Exam 11: Regression Analysis: Statistical Inference82 Questions
Exam 12: Time Series Analysis and Forecasting106 Questions
Exam 13: Introduction to Optimization Modeling97 Questions
Exam 14: Optimization Models114 Questions
Exam 15: Introduction to Simulation Modeling82 Questions
Exam 16: Simulation Models102 Questions
Exam 17: Data Mining20 Questions
Exam 18: Importing Data Into Excel19 Questions
Exam 19: Analysis of Variance and Experimental Design20 Questions
Exam 20: Statistical Process Control20 Questions
Select questions type
All linear programming problems should have a unique solution, if they can be solved.
(True/False)
4.9/5  (31)
(31)
There are generally two steps in solving an optimization problem: model development and optimization.
(True/False)
4.9/5  (29)
(29)
Linear programming is a subset of a larger class of models called:
(Multiple Choice)
4.8/5  (38)
(38)
It helps to ensure that Solver can find a solution to a linear programming problem if the model is well-scaled, that is, if all of the numbers are of roughly the same magnitude.
(True/False)
4.8/5  (39)
(39)
Consider the following linear programming problem: Maximize 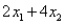 Subject to:
Subject to: 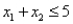
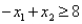
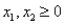 The above linear programming problem:
The above linear programming problem:
(Multiple Choice)
4.9/5  (32)
(32)
(A) Determine how to minimize the cost of meeting the demand for the next three weeks.
(B) Revise the model in (A) so that the demands are of the form 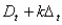 , where
, where 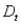 is the original demand in month t, k is a factor, and
is the original demand in month t, k is a factor, and 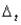 is an amount of change in month t. Formulate the model in such away that you can use the SolverTable add-in to analyze changes in the amounts produced and the total cost when k varies from 0 to 10 in 1-unit increments, for any fixed values of the
is an amount of change in month t. Formulate the model in such away that you can use the SolverTable add-in to analyze changes in the amounts produced and the total cost when k varies from 0 to 10 in 1-unit increments, for any fixed values of the 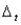 's. For example, try this when
's. For example, try this when 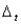 = 2,
= 2, 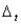 = 5, and
= 5, and 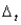 = 3. Describe the behavior you observe in the table. Can you find any "reasonable"
= 3. Describe the behavior you observe in the table. Can you find any "reasonable" 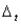 's that induce positive production levels in week 3?
's that induce positive production levels in week 3?
(Essay)
4.9/5  (39)
(39)
(A) Determine how to minimize the net cost incurred in meeting the demands for the next four months.
(B) Starting with the optimal solution to (A), use SolverTable add-in to see what happens to the decision variables and the total cost when the initial inventory varies from 0 (the implied value in (A)) to 100 in 10-units increments. How much lower would the total cost be if the company started with 10 units in inventory, rather than none? Would the same cost decrease occur for every 10-init increase in initial inventory?
(Essay)
4.8/5  (36)
(36)
Suppose a company sells two different products, x and y, for net profits of $5 per unit and $10 per unit, respectively. The slope of the line representing the objective function is:
(Multiple Choice)
4.8/5  (32)
(32)
Suppose the allowable increase and decrease for shadow price for a constraint are $25 (increase) and $10 (decrease). If the right hand side of that constraint were to increase by $10, the optimal value of the objective function would change.
(True/False)
4.9/5  (40)
(40)
In most cases, when solving linear programming problems, we want the decision variables to be:
(Multiple Choice)
4.8/5  (41)
(41)
A rolling planning horizon is a multiperiod model where only the decision in the first period is implemented, and then a new multiperiod model is solved in succeeding periods.
(True/False)
4.8/5  (42)
(42)
The proportionality property of LP models means that if the level of any activity is multiplied by a constant factor, then the contribution of this activity to the objective function, or to any of the constraints in which the activity is involved, is multiplied by the same factor.
(True/False)
4.9/5  (39)
(39)
A marketing research professor is conducting a telephone survey and needs to contact at least 160 wives, 140 husbands, 110 single adult males, and 120 single adult females. It costs $2 to make a daytime call and $4 (because of higher labor costs) to make an evening call. The table shown below lists the expected results. For example, 10% of all daytime calls are answered by a single male, and 15% of all evening calls are answered by a single female. Because of a limited staff, at most half of all phone calls can be evening calls. Determine how to minimize the cost of completing the survey.  -What are the decision variables in this problem?
-What are the decision variables in this problem?
(Essay)
4.8/5  (35)
(35)
Find an optimal solution to the problem, assuming that the company will not produce any units in either month that it cannot sell in that month. What is the production plan, and what is the total revenue?
(Essay)
5.0/5  (40)
(40)
A marketing research professor is conducting a telephone survey and needs to contact at least 160 wives, 140 husbands, 110 single adult males, and 120 single adult females. It costs $2 to make a daytime call and $4 (because of higher labor costs) to make an evening call. The table shown below lists the expected results. For example, 10% of all daytime calls are answered by a single male, and 15% of all evening calls are answered by a single female. Because of a limited staff, at most half of all phone calls can be evening calls. Determine how to minimize the cost of completing the survey.  -(A) What is the objective function in this problem?
(B) What are the constraints in this problem? Write an algebraic expression for each.
(C) Find an optimal solution to the problem using the formulation given in (A) and (B). What is the call plan, and what is the total cost?
(D) Implement the model in (C) in Excel Solver and obtain an answer report. Which constraints are binding on the optimal solution?
(E) Obtain a sensitivity report for the model in (D). If the professor could cut the cost of evening calls from $4 to $3, what would the new calling plan be?
(F) Again using the sensitivity report obtained for (E), suppose the professor could get by with just 100 calls for single females. What would the call costs be in that case? Explain your answer.
-(A) What is the objective function in this problem?
(B) What are the constraints in this problem? Write an algebraic expression for each.
(C) Find an optimal solution to the problem using the formulation given in (A) and (B). What is the call plan, and what is the total cost?
(D) Implement the model in (C) in Excel Solver and obtain an answer report. Which constraints are binding on the optimal solution?
(E) Obtain a sensitivity report for the model in (D). If the professor could cut the cost of evening calls from $4 to $3, what would the new calling plan be?
(F) Again using the sensitivity report obtained for (E), suppose the professor could get by with just 100 calls for single females. What would the call costs be in that case? Explain your answer.
(Essay)
4.8/5  (36)
(36)
Suppose a constraint has this equation: 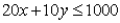 Then the slope of the constraint line is -2.
Then the slope of the constraint line is -2.
(True/False)
5.0/5  (39)
(39)
What is the equation of the line representing this constraint? 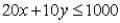
(Multiple Choice)
4.9/5  (41)
(41)
Adam Enterprises manufactures two products. Each product can be produced on either of two machines. The time (in hours) required to make each product on each machine is shown below:  Each month, 500 hours of time are available on each machine, and also customers are willing to buy up to the quantities of each product at the prices shown below:
Each month, 500 hours of time are available on each machine, and also customers are willing to buy up to the quantities of each product at the prices shown below:  The company's goal is to maximize the revenue obtained from selling units during the next two months.
-(A) Determine how the company can meet its goal. Assume that Adam will not produce any units in either month that it cannot sell in that month.
(B) Referring to (A), suppose Adam wants to see what will happen if customer demands for each product in each month simultaneously change by a factor 1 + k. Revise the model so that you can use the SolverTable add-in to investigate the effect of this change on total revenue as k varies from -0.3 to 0.3 in increments of 0.1. Does revenue change in a linear manner over this range? Can you explain intuitively why it changes in the way it does?
The company's goal is to maximize the revenue obtained from selling units during the next two months.
-(A) Determine how the company can meet its goal. Assume that Adam will not produce any units in either month that it cannot sell in that month.
(B) Referring to (A), suppose Adam wants to see what will happen if customer demands for each product in each month simultaneously change by a factor 1 + k. Revise the model so that you can use the SolverTable add-in to investigate the effect of this change on total revenue as k varies from -0.3 to 0.3 in increments of 0.1. Does revenue change in a linear manner over this range? Can you explain intuitively why it changes in the way it does?
(Essay)
4.9/5  (44)
(44)
One of the tasks that you can perform with linear programming and a spreadsheet model is developing a user interface to make it easier for someone who is not an expert in using linear programming. The output can be a report that explains the optimal policy in non-technical terms. The type of system being described is called a(n):
(Multiple Choice)
4.8/5  (34)
(34)
Showing 41 - 60 of 97
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)