Exam 15: Multiple Regression
Exam 1: Data and Statistics98 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays62 Questions
Exam 3: Descriptive Statistics: Numerical Measures173 Questions
Exam 4: Introduction to Probability138 Questions
Exam 5: Discrete Probability Distributions123 Questions
Exam 6: Continuous Probability Distributions174 Questions
Exam 7: Sampling and Sampling Distributions133 Questions
Exam 8: Interval Estimation137 Questions
Exam 9: Hypothesis Tests148 Questions
Exam 10: Inference About Means and Proportions With Two Populations121 Questions
Exam 11: Inferences About Population Variances90 Questions
Exam 12: Comparing Multiple Proportions, Test of Independence and Goodness of Fit90 Questions
Exam 13: Experimental Design and Analysis of Variance115 Questions
Exam 14: Simple Linear Regression146 Questions
Exam 15: Multiple Regression115 Questions
Exam 16: Regression Analysis: Model Building76 Questions
Exam 17: Time Series Analysis and Forecasting68 Questions
Exam 18: Nonparametric Methods81 Questions
Exam 19: Statistical Methods for Quality Control29 Questions
Exam 20: Index Numbers52 Questions
Exam 21: Decision Analysis on Website65 Questions
Exam 22: Sample Survey on Website63 Questions
Select questions type
A term used to describe the case when the independent variables in a multiple regression model are correlated is
(Multiple Choice)
4.9/5  (36)
(36)
Exhibit 15-6
Below you are given a partial computer output based on a sample of 16 observations. 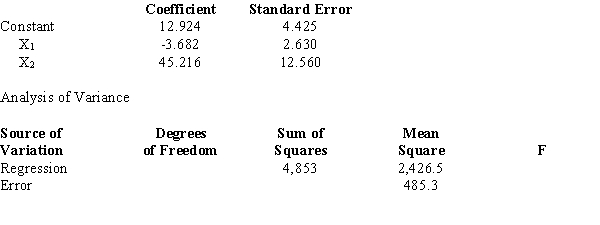 -Refer to Exhibit 15-6. The t value obtained from the table which is used to test an individual parameter at the 1% level is
-Refer to Exhibit 15-6. The t value obtained from the table which is used to test an individual parameter at the 1% level is
(Multiple Choice)
4.9/5  (31)
(31)
In a multiple regression analysis involving 10 independent variables and 81 observations, SST = 120 and SSE = 42. The coefficient of determination is
(Multiple Choice)
5.0/5  (26)
(26)
Below you are given a partial computer output based on a sample of 12 observations relating the number of personal computers sold by a computer shop per month (Y), unit price (X1 in $1,000) and the number of advertising spots (X2) they used on a local television station.  a.At = 0.05 level of significance, test to determine if the model is significant. That is, determine if there exists a significant relationship between the independent variables and the dependent variable.
b.Determine the multiple coefficient of determination.
c.Determine the adjusted multiple coefficient of determination.
a.At = 0.05 level of significance, test to determine if the model is significant. That is, determine if there exists a significant relationship between the independent variables and the dependent variable.
b.Determine the multiple coefficient of determination.
c.Determine the adjusted multiple coefficient of determination.
(Essay)
4.8/5  (30)
(30)
A regression model involving 8 independent variables for a sample of 69 periods resulted in the following sum of squares.
SSE = 306
SST = 1800
a.Compute the coefficient of determination.
b.At = 0.05, test to determine whether or not the model is significant.
(Essay)
4.9/5  (37)
(37)
The following is part of the results of a regression analysis involving sales (Y in millions of dollars), advertising expenditures (X1 in thousands of dollars), and number of sales people (X2) for a corporation:  a.At = 0.05 level of significance, test to determine if the model is significant. That is, determine if there exists a significant relationship between the independent variables and the dependent variable.
b.Determine the multiple coefficient of determination.
c.Determine the adjusted multiple coefficient of determination.
d.What has been the sample size for this regression analysis?
a.At = 0.05 level of significance, test to determine if the model is significant. That is, determine if there exists a significant relationship between the independent variables and the dependent variable.
b.Determine the multiple coefficient of determination.
c.Determine the adjusted multiple coefficient of determination.
d.What has been the sample size for this regression analysis?
(Essay)
4.8/5  (32)
(32)
A microcomputer manufacturer has developed a regression model relating his sales (Y in $10,000s) with three independent variables. The three independent variables are price per unit (Price in $100s), advertising (ADV in $1,000s) and the number of product lines (Lines). Part of the regression results is shown below.  a. Use the above results and write the regression equation that can be used to predict sales.
b.If the manufacturer has 10 product lines, advertising of $40,000, and the price per unit is $3,000, what is your estimate of their sales? Give your answer in dollars.
c.Compute the coefficient of determination and fully interpret its meaning.
d.At = 0.05, test to see if there is a significant relationship between sales and unit price.
e.At = 0.05, test to see if there is a significant relationship between sales and the number of product lines.
f. Is the regression model significant? (Perform an F test.)
g. Fully interpret the meaning of the regression (coefficient of price) per unit that is, the slope for the price per unit.
h. What has been the sample size for this analysis?
a. Use the above results and write the regression equation that can be used to predict sales.
b.If the manufacturer has 10 product lines, advertising of $40,000, and the price per unit is $3,000, what is your estimate of their sales? Give your answer in dollars.
c.Compute the coefficient of determination and fully interpret its meaning.
d.At = 0.05, test to see if there is a significant relationship between sales and unit price.
e.At = 0.05, test to see if there is a significant relationship between sales and the number of product lines.
f. Is the regression model significant? (Perform an F test.)
g. Fully interpret the meaning of the regression (coefficient of price) per unit that is, the slope for the price per unit.
h. What has been the sample size for this analysis?
(Essay)
4.9/5  (46)
(46)
The following is part of the results of a regression analysis involving sales (Y in millions of dollars), advertising expenditures (X1 in thousands of dollars), and number of salespeople (X2) for a corporation. The regression was performed on a sample of 10 observations.  a.Write the regression equation.
b.Interpret the coefficients of the estimated regression equation found in Part (a).
c.At =0.05, test for the significance of the coefficient of advertising.
d.At =0.05, test for the significance of the coefficient of number of salespeople.
e.If the company uses $50,000 in advertisement and has 800 salespersons, what are the expected sales? Give your answer in dollars.
a.Write the regression equation.
b.Interpret the coefficients of the estimated regression equation found in Part (a).
c.At =0.05, test for the significance of the coefficient of advertising.
d.At =0.05, test for the significance of the coefficient of number of salespeople.
e.If the company uses $50,000 in advertisement and has 800 salespersons, what are the expected sales? Give your answer in dollars.
(Essay)
4.9/5  (34)
(34)
A measure of the effect of an unusual x value on the regression results is called
(Multiple Choice)
4.7/5  (33)
(33)
Exhibit 15-2
A regression model between sales (Y in $1,000), unit price (X1 in dollars) and television advertisement (X2 in dollars) resulted in the following function: 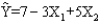 For this model SSR = 3500, SSE = 1500, and the sample size is 18.
-Refer to Exhibit 15-2. To test for the significance of the model, the p-value is
For this model SSR = 3500, SSE = 1500, and the sample size is 18.
-Refer to Exhibit 15-2. To test for the significance of the model, the p-value is
(Multiple Choice)
4.9/5  (39)
(39)
Exhibit 15-8
The following estimated regression model was developed relating yearly income (Y in $1,000s) of 30 individuals with their age (X1) and their gender (X2) (0 if male and 1 if female). 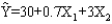 Also provided are SST = 1,200 and SSE = 384.
-Refer to Exhibit 15-8. From the above function, it can be said that the expected yearly income of
Also provided are SST = 1,200 and SSE = 384.
-Refer to Exhibit 15-8. From the above function, it can be said that the expected yearly income of
(Multiple Choice)
4.9/5  (35)
(35)
Exhibit 15-6
Below you are given a partial computer output based on a sample of 16 observations.  -Refer to Exhibit 15-6. The interpretation of the coefficient of X1 is that
-Refer to Exhibit 15-6. The interpretation of the coefficient of X1 is that
(Multiple Choice)
4.9/5  (27)
(27)
A variable that takes on the values of 0 or 1 and is used to incorporate the effect of qualitative variables in a regression model is called
(Multiple Choice)
4.8/5  (45)
(45)
Exhibit 15-1
In a regression model involving 44 observations, the following estimated regression equation was obtained. 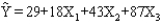 For this model SSR = 600 and SSE = 400.
-Refer to Exhibit 15-1. The computed F statistics for testing the significance of the above model is
For this model SSR = 600 and SSE = 400.
-Refer to Exhibit 15-1. The computed F statistics for testing the significance of the above model is
(Multiple Choice)
4.8/5  (29)
(29)
Exhibit 15-6
Below you are given a partial computer output based on a sample of 16 observations.  -Refer to Exhibit 15-6. The test statistic used to determine if there is a relationship among the variables equals
-Refer to Exhibit 15-6. The test statistic used to determine if there is a relationship among the variables equals
(Multiple Choice)
4.9/5  (35)
(35)
A measure of goodness of fit for the estimated regression equation is the
(Multiple Choice)
4.7/5  (37)
(37)
A multiple regression analysis between yearly income (Y in $1,000s), college grade point average (X1), age of the individuals (X2), and the gender of the individual (X3; zero representing female and one representing male) was performed on a sample of 10 people, and the following results were obtained. 
 a. Write the regression equation for the above.b. Interpret the meaning of the coefficient of X3.
c. Compute the coefficient of determination.
d. Is the coefficient of X1 significant? Use = 0.05.
e. Is the coefficient of X2 significant? Use = 0.05.
f. Is the coefficient of X3 significant? Use = 0.05.
g. Perform an F test and determine whether or not the model is significant.
a. Write the regression equation for the above.b. Interpret the meaning of the coefficient of X3.
c. Compute the coefficient of determination.
d. Is the coefficient of X1 significant? Use = 0.05.
e. Is the coefficient of X2 significant? Use = 0.05.
f. Is the coefficient of X3 significant? Use = 0.05.
g. Perform an F test and determine whether or not the model is significant.
(Essay)
4.8/5  (42)
(42)
The following regression model has been proposed to predict sales at a fast food outlet.  a.What is the interpretation of 15 (the coefficient of X3) in the regression equation?
b.Predict sales for a store with 2 competitors, a population of 10,000 within one mile, and one drive-up window (give the answer in dollars).
c.Predict sales for the store with 2 competitors, a population of 10,000 within one mile, and no drive-up window (give the answer in dollars).
a.What is the interpretation of 15 (the coefficient of X3) in the regression equation?
b.Predict sales for a store with 2 competitors, a population of 10,000 within one mile, and one drive-up window (give the answer in dollars).
c.Predict sales for the store with 2 competitors, a population of 10,000 within one mile, and no drive-up window (give the answer in dollars).
(Essay)
4.8/5  (29)
(29)
Showing 41 - 60 of 115
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)