Exam 6: Continuous Probability Distributions
Exam 1: Data and Statistics98 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays62 Questions
Exam 3: Descriptive Statistics: Numerical Measures173 Questions
Exam 4: Introduction to Probability138 Questions
Exam 5: Discrete Probability Distributions123 Questions
Exam 6: Continuous Probability Distributions174 Questions
Exam 7: Sampling and Sampling Distributions133 Questions
Exam 8: Interval Estimation137 Questions
Exam 9: Hypothesis Tests148 Questions
Exam 10: Inference About Means and Proportions With Two Populations121 Questions
Exam 11: Inferences About Population Variances90 Questions
Exam 12: Comparing Multiple Proportions, Test of Independence and Goodness of Fit90 Questions
Exam 13: Experimental Design and Analysis of Variance115 Questions
Exam 14: Simple Linear Regression146 Questions
Exam 15: Multiple Regression115 Questions
Exam 16: Regression Analysis: Model Building76 Questions
Exam 17: Time Series Analysis and Forecasting68 Questions
Exam 18: Nonparametric Methods81 Questions
Exam 19: Statistical Methods for Quality Control29 Questions
Exam 20: Index Numbers52 Questions
Exam 21: Decision Analysis on Website65 Questions
Exam 22: Sample Survey on Website63 Questions
Select questions type
Exhibit 6-4
f(x) =(1/10) e-x/10 x  0
-Refer to Exhibit 6-4. The probability that x is between 3 and 6 is
0
-Refer to Exhibit 6-4. The probability that x is between 3 and 6 is
(Multiple Choice)
4.7/5  (32)
(32)
Z is a standard normal random variable. Compute the following probabilities.
a.P(-1.33 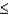 Z
Z 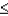 1.67)
b.P(1.23
1.67)
b.P(1.23 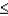 Z
Z 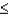 1.55)
c.P(Z
1.55)
c.P(Z  2.32)
d.P(Z
2.32)
d.P(Z  -2.08)
e.P(Z
-2.08)
e.P(Z 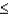 -1.08)
-1.08)
(Short Answer)
4.8/5  (30)
(30)
Exhibit 6-8
The life expectancy of a particular brand of tire is normally distributed with a mean of 40,000 and a standard deviation of 5,000 miles.
-Refer to Exhibit 6-8. What is the probability that a randomly selected tire will have a life of at least 30,000 miles?
(Multiple Choice)
5.0/5  (33)
(33)
A major credit card company has determined that its customers charge an average of $280 per month on their accounts with a standard deviation of $20.
a.What percentage of the customers charges more than $275 per month?
b.What percentage of the customers charges less than $243 per month?
c.What percentage of the customers charges between $241 and $301.60 per month?
(Short Answer)
4.8/5  (38)
(38)
A professor at a local university noted that the grades of her students were normally distributed with a mean of 78 and a standard deviation of 10.
a.The professor has informed us that 16.6 percent of her students received grades of A. What is the minimum score needed to receive a grade of A?
b.If 12.1 percent of her students failed the course and received F's, what was the maximum score among those who received an F?
c.If 33 percent of the students received grades of B or better (i.e., A's and B's), what is the minimum score of those who received a B?
(Short Answer)
4.8/5  (32)
(32)
The SAT scores of students are normally distributed with a mean of 950 and a standard deviation of 200.
a.Nancy Bright's SAT score was 1390. What percentage of students have scores higher than Nancy Bright?
b.What percentage of students score between 1100 and 1200?
c.What are the minimum and the maximum values of the middle 87.4% of the scores?
d.There were 165 students who scored above 1432. How many students took the SAT?
(Short Answer)
4.7/5  (42)
(42)
Given that Z is a standard normal random variable, what is the probability that -2.51 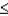 Z
Z 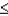 F -1.53?
F -1.53?
(Multiple Choice)
4.9/5  (28)
(28)
A random variable X is uniformly distributed between 45 and 150.
a.Determine the probability of X = 48.
b.What is the probability of X 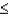 60?
c.What is the probability of X
60?
c.What is the probability of X  50?
d.Determine the expected vale of X and its standard deviation.
50?
d.Determine the expected vale of X and its standard deviation.
(Short Answer)
4.8/5  (37)
(37)
The salaries of the employees of a corporation are normally distributed with a mean of $25,000 and a standard deviation of $5,000.
a.What is the probability that a randomly selected employee will have a starting salary of at least $31,000?
b.What percentage of employees has salaries of less than $12,200?
c.What are the minimum and the maximum salaries of the middle 95% of the employees?
d.If sixty-eight of the employees have incomes of at least $35,600, how many individuals are employed in the corporation?
(Essay)
4.9/5  (41)
(41)
Z is a standard normal random variable. The P(1.05 < Z < 2.13) equals
(Multiple Choice)
4.9/5  (38)
(38)
Approximate the following binomial probabilities by the use of normal approximation. Twenty percent of students who finish high school do not go to college. What is the probability that in a sample of 80 high school students
a.exactly 10 will not go to college?
b.70 or more will go to college?
c.fourteen or fewer will not go to college?
(Short Answer)
4.8/5  (32)
(32)
A standard normal distribution is a normal distribution with
(Multiple Choice)
4.8/5  (31)
(31)
Given that Z is a standard normal random variable, what is the probability that Z  -2.12?
-2.12?
(Multiple Choice)
4.8/5  (27)
(27)
Exhibit 6-6
The starting salaries of individuals with an MBA degree are normally distributed with a mean of $40,000 and a standard deviation of $5,000.
-Refer to Exhibit 6-6. What percentage of MBA's will have starting salaries of $34,000 to $46,000?
(Multiple Choice)
5.0/5  (40)
(40)
The time it takes a worker on an assembly line to complete a task is exponentially distributed with a mean of 8 minutes.
a.What is the probability density function for the time it takes to complete the task?
b.What is the probability that it will take a worker less than 4 minutes to complete the task?
c.What is the probability that it will take a worker between 6 and 10 minutes to complete the task?
(Essay)
4.8/5  (35)
(35)
Given that Z is a standard normal random variable, what is the value of Z if the area to the right of Z is 0.5?
(Multiple Choice)
4.8/5  (36)
(36)
An airline has determined that 20% of its international flights are not on time. Use the normal approximation to the binomial distribution to answer the following questions. What is the probability that of the next 80 international flights
a.fifteen or less will not be on time?
b.eighteen or more will not be on time?
c.exactly 17 will not be on time?
(Short Answer)
4.8/5  (32)
(32)
Given that Z is a standard normal random variable, what is the value of Z if the area between -Z and Z is 0.901?
(Multiple Choice)
4.9/5  (30)
(30)
Showing 121 - 140 of 174
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)