Exam 13: A Fundamental Tool- Vectors
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
Let ABCDEF be a regular hexagon.Express the vectors and in terms of .
(Essay)
4.9/5  (37)
(37)
Suppose that and are non-zero vectors and .Then what MUST be true about and ?
(Multiple Choice)
4.9/5  (39)
(39)
Find the vector in 3-space which satisfies both of the following conditions.
(a) (b)
(Essay)
4.8/5  (35)
(35)
Two boats leave a harbor at the same time.Boat A cruises northwest at a rate of 17 knots (nautical miles per hour).Boat B cruises north at a rate of 21 knots.
(a)Find the displacement vector from boat A to boat B half an hour later.
(b)For the passengers in boat A, what does the velocity of boat B appear to be?
(Essay)
4.9/5  (36)
(36)
Compute the area of the triangle with vertices A(0, 0, 0), B(3, 3, 0), and C(3, 6, 3).
(Essay)
4.9/5  (34)
(34)
Given that and are non-zero vectors and that , then which of the following MUST be true? Select all that apply.
(Multiple Choice)
4.9/5  (45)
(45)
The vector is parallel to the x-axis where and are shown below (both and are in the xy-plane). 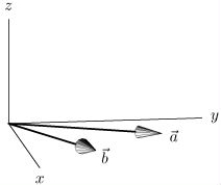
(True/False)
4.9/5  (28)
(28)
Showing 41 - 60 of 107
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)