Exam 2: Methods for Describing Sets of Data

A study was designed to investigate the effects of two variables - (1)a studentʹs level of mathematical anxiety and (2)teaching method - on a studentʹs achievement in a mathematics Course. Students who had a low level of mathematical anxiety were taught using the traditional Expository method. These students obtained a mean score of 430 with a standard deviation of 20 On a standardized test. Assuming a non-mound-shaped distribution, what percentage of the Students scored over 490?

The mean of a data set is at the 50th percentile.

A small computing center has found that the number of jobs submitted per day to its computers has a distribution that is approximately mound-shaped and symmetric, with a mean of 61 jobs and a standard deviation of 8. On what percentage of days do the number of jobs submitted exceed 69?

A recent survey was conducted to compare the cost of solar energy to the cost of gas or electric energy. Results of the survey revealed that the distribution of the amount of the monthly utility bill Of a 3-bedroom house using gas or electric energy had a mean of $110 and a standard deviation of $14. Three solar homes reported monthly utility bills of $63, $64, and $60. Which of the following Statements is true?

The calculator screens summarize a data set. 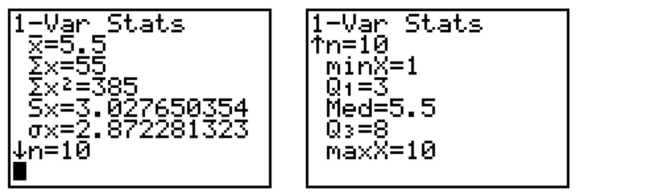a. Identify the mean and the sample standard deviation. Round to one place after the decimal, where necessary. b. Find the interval that corresponds to measurements within two standard deviations of the mean.

If a z-score is 0 or near 0, the measurement is located at or near the mean.

The amount spent on textbooks for the fall term was recorded for a sample of five hundred university students. The mean expenditure was calculated to be $500 and the median expenditure Was calculated to be $425. Which of the following interpretations of the mean is correct?

If a sample has mean 0 and standard deviation 1, then for every measurement x in the sample the z-score of x is x itself.

The z-score uses the quartiles to identify outliers in a data set.

If nothing is known about the shape of a distribution, what percentage of the observations fall within 3 standard deviations of the mean?

Both Chebyshevʹs rule and the empirical rule guarantee that no data item will be more than four standard deviations from the mean.

At the U.S. Open Tennis Championship a statistician keeps track of every serve that a player hits during the tournament. The statistician reported that the mean serve speed of a particular player Was 100 miles per hour (mph)and the standard deviation of the serve speeds was 15 mph. Using The z-score approach for detecting outliers, which of the following serve speeds would represent Outliers in the distribution of the playerʹs serve speeds? Speeds: 50 mph, 80 mph, and 105 mph

The sample variance and standard deviation can be calculated using only the sum of the data, $\sum { x }$ and the sample size, n.

The data show the total number of medals (gold, silver, and bronze)won by each country winning at least one gold medal in the Winter Olympics. Find the mean, median, and mode of the numbers of medals won by these countries. 1 2 3 3 4 9 9 11 11 11 14 14 19 22 23 24 25 29

Given a data set, which of the following is most likely to be the percentage of data within three standard deviations of the mean?

In a symmetric and mound shaped distribution, we expect the values of the mean, median, and mode to differ greatly from one another.

Calculate the mean of a sample for which $\sum x = 196$ and n=8

The following is a list of 25 measurements: 12 18 14 17 19 16 14 18 15 17 11 13 14 11 16 18 15 13 17 15 14 19 12 16 17 How many of the measurements fall within one standard deviation of the mean?

A small computing center has found that the number of jobs submitted per day to its computers has a distribution that is approximately mound-shaped and symmetric, with a mean of 69 jobs And a standard deviation of 8. Where do we expect approximately 95% of the distribution to fall?

At the U.S. Open Tennis Championship a statistician keeps track of every serve that a player hits during the tournament. The statistician reported that the mean serve speed of a particular player Was 99 miles per hour (mph)and the standard deviation of the serve speeds was 14 mph. Assume That the statistician also gave us the information that the distribution of the serve speeds was Mound-shaped and symmetric. What proportion of the playerʹs serves was between 113 mph and 141 mph?