Exam 2: Methods for Describing Sets of Data

The calculator screens summarize a data set. 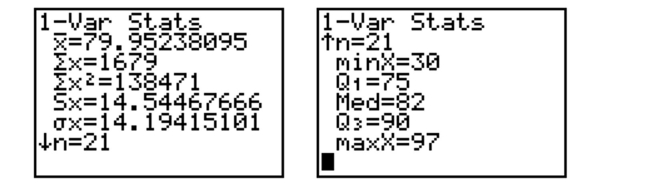a. How many data items are in the set? b. What is the sum of the data? c. Identify the mean, median, and mode, if possible.

The amount spent on textbooks for the fall term was recorded for a sample of five university students - $400, $350, $600, $525, and $450. Calculate the value of the sample mean for the data.

A survey was conducted to determine how people feel about the quality of programming available on television. Respondents were asked to rate the overall quality from 0 (no quality at all)to 100 (extremely good quality). The stem-and-leaf display of the data is shown below. Stem Leaf 3 2 3 4 0 3 4 7 8 9 9 9 5 0 1 1 2 3 4 5 6 1 2 5 6 6 7 4 9 8 9 9 What percentage of the respondents rated overall television quality as very good (regarded as Ratings of 80 and above)?

A recent survey was conducted to compare the cost of solar energy to the cost of gas or electric energy. Results of the survey revealed that the distribution of the amount of the monthly utility bill Of a 3-bedroom house using gas or electric energy had a mean of $143 and a standard deviation of $8. If the distribution can be considered mound-shaped and symmetric, what percentage of homes Will have a monthly utility bill of more than $135?

In a distribution that is skewed to the right, what is the relationship of the mean, median, and mode?

The box plot shown below was constructed for the amount of soda that was poured by a filling machine into 12-ounce soda cans at a local soda bottling company. We see that one soda can received 12.15 ounces of soda on the plot above. Based on the box plot Presented, how would you classify this observation?

A recent survey was conducted to compare the cost of solar energy to the cost of gas or electric energy. Results of the survey revealed that the distribution of the amount of the monthly utility bill of a 3-bedroom house using gas or electric energy had a mean of $118.00 and a standard deviation of $15.00. Assuming the distribution is mound-shaped and symmetric, would you expect to see a 3-bedroom house using gas or electric energy with a monthly utility bill of $230.50? Explain.

At the U.S. Open Tennis Championship a statistician keeps track of every serve that a player hits during the tournament. The statistician reported that the mean serve speed was 100 miles per hour (mph)and the standard deviation of the serve speeds was 15 mph. If nothing is known about the Shape of the distribution, what percentage of the playerʹs serve speeds are less than 70 mph?

During one recent year, U.S. consumers redeemed 6.16 billion manufacturersʹ coupons and saved themselves $2.27 billion. Calculate and interpret the mean savings per coupon.

In general, the sample mean is a better estimator of the population mean for larger sample sizes.

Each year advertisers spend billions of dollars purchasing commercial time on network television. In the first 6 months of one year, advertisers spent $1.1 billion. Who were the largest spenders? In a recent article, the top 10 leading spenders and how much each spent (in million of dollars)were listed: Company A \ 72.2 Company F \ 27.2 Company B 63 Company G 24.2 Company C 57.2 Company H 22.5 Company D 55.3 Company I 22.1 Company E 30.5 Company J 19.4 Calculate the mean and median for the data.

Compute $\mathrm { s } ^ { 2 }$ and s for the data set: $\frac { 1 } { 10 } , \frac { 3 } { 5 } , \frac { 1 } { 10 } , \frac { 1 } { 5 } , \frac { 7 } { 10 } , \frac { 3 } { 10 } .$

In skewed distributions, the mean is the best measure of the center of the distribution since it is least affected by extreme observations.

At the U.S. Open Tennis Championship a statistician keeps track of every serve that a player hits during the tournament. The statistician reported that the mean serve speed of a particular player Was 105 miles per hour. Suppose that the statistician indicated that the serve speed distribution Was skewed to the left. Which of the following values is most likely the value of the median serve Speed?

A Pareto diagram is a pie chart where the slices are arranged from largest to smallest in a counterclockwise direction.

The total points scored by a basketball team for each game during its last season have been summarized in the table below. Identify the modal class of the distribution of scores. Score Frequency 41-60 3 61-80 8 81-100 12 101-120 7

Summary information is given for the weights (in pounds)of 1000 randomly sampled tractor trailers. MIN: 4013 25\%: 5613 MAX: 10,613 75\%: 8613 AVE: 7013 Std. Dev.: 1400 Find the percentage of tractor trailers with weights between 5613 and 8613 pounds.

Explain how it can be misleading to report only the mean of a distribution without any measure of the variability.

Fill in the blank. One advantage of the __________ is that the actual data values are retained in the graphical summarization of the data.

The total points scored by a basketball team for each game during its last season have been summarized in the table below. Score Frequency 41-60 3 61-80 8 81-100 12 101-120 7 a. Explain why you cannot use the information in the table to construct a stem-and-leaf display for the data. b. Construct a histogram for the scores.