Exam 11: The Analysis of Variance
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
The purpose of designing a randomized block experiment is to reduce the between-treatments variation (SST) to more easily detect differences between the treatment means.
(True/False)
4.8/5  (34)
(34)
Which of the following statements about ANOVA completely randomized design is correct?
(Multiple Choice)
4.8/5  (41)
(41)
Which of the following is not true of Tukey's Multiple Comparison Method?
(Multiple Choice)
4.7/5  (43)
(43)
A study was conducted to compare automobile gasoline mileage for three brands of gasoline, A, B, and C. Four automobiles, all of the same make and model, were used in the experiment, and each gasoline brand was tested in each automobile. Using each brand in the same automobile has the effect of eliminating (blocking out) automobile-to-automobile variability. The data (in miles per gallon) are as follows:  Use Minitab or Excel to generate a summary table and the ANOVA table.
Do the data provide sufficient evidence to indicate a difference in mean mileage per gallon for the three brands of gasoline?
F = ______________
p-value = ______________
There ______________ sufficient evidence to indicate a difference in mean mileage per gallon for the three brands of gasoline.
Is there evidence of a difference in mean mileage for the four automobiles?
F = ______________
p-value = ______________
There ______________ sufficient evidence to indicate a difference in mean mileage per gallon for the four automobiles.
Use Minitab or Excel to generate a summary table and the ANOVA table.
Do the data provide sufficient evidence to indicate a difference in mean mileage per gallon for the three brands of gasoline?
F = ______________
p-value = ______________
There ______________ sufficient evidence to indicate a difference in mean mileage per gallon for the three brands of gasoline.
Is there evidence of a difference in mean mileage for the four automobiles?
F = ______________
p-value = ______________
There ______________ sufficient evidence to indicate a difference in mean mileage per gallon for the four automobiles.
(Short Answer)
4.7/5  (30)
(30)
In one-way ANOVA, the sum of the squared deviations of each individual sample observation (regardless of the sample to which it belongs) from the mean of all observations is called:
(Multiple Choice)
4.8/5  (41)
(41)
The randomized block design with two treatments is equivalent to a non-directional dependent samples z-test.
(True/False)
4.9/5  (33)
(33)
In a one-way ANOVA, if 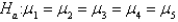 and a sample of size 25 is selected at random from each of the five populations, then which of the following is the correct critical value at
and a sample of size 25 is selected at random from each of the five populations, then which of the following is the correct critical value at 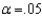 ?
?
(Multiple Choice)
4.8/5  (36)
(36)
In a two-way factor ANOVA, the total sum of squares can be partitioned into four parts: the variation due to factor A, the variation due to factor B, the error variation, and the variation due to blocking.
(True/False)
4.8/5  (32)
(32)
In ANOVA, a factor is an independent variable whose values are controlled and varied by the experimenter, while a level is the intensity setting of a factor.
(True/False)
4.8/5  (41)
(41)
A randomized block experiment having five treatments and four blocks produced the following values: Total SS = 1500, SST = 275, SSE = 153. The value of MSB must be 268.
(True/False)
4.9/5  (37)
(37)
Two-factor or two-way ANOVA is one of several versions of the analysis of variance, which controls extraneous factors by using the randomized block design.
(True/False)
4.9/5  (34)
(34)
The calculated value of F in a one-way ANOVA is 7.88. The numerator and denominator degrees of freedom are 3 and 9, respectively. The most accurate statement to be made about the p-value is that p-value < 0.01.
(True/False)
4.9/5  (37)
(37)
In the analysis of variance, the sum of all samples' sums of squared deviations of individual observations from their sample mean equals the error mean square.
(True/False)
4.8/5  (39)
(39)
In a completely randomized design for ANOVA, the numerator and denominator degrees of freedom are 4 and 25, respectively. The total number of observations must equal:
(Multiple Choice)
4.7/5  (32)
(32)
The analysis of variance (ANOVA) technique analyzes the variance of the data to determine whether differences exist between the population variances.
(True/False)
4.9/5  (40)
(40)
An experimental plan that creates one treatment group for each treatment and then randomly assigns each experimental unit to one of these groups is called:
(Multiple Choice)
4.9/5  (48)
(48)
Multiple comparison methods are used in one-way ANOVA and if the null hypothesis states that there is no difference between the treatment means, the null hypothesis is:
(Multiple Choice)
4.7/5  (40)
(40)
In analysis of variances, the sum of squares for treatments (SST) is zero when all the sample means are equal.
(True/False)
4.9/5  (49)
(49)
A researcher at Michigan State University (MSU) wanted to determine whether different building signs (building maps versus wall signage) affect the total amount of time visitors require to reach their destination and whether that time depends on whether the starting location is inside or outside the building. Three subjects were assigned to each of the combinations of signs and starting locations, and travel time in seconds from beginning to destination was recorded. A partial computer output of the appropriate analysis is given below: 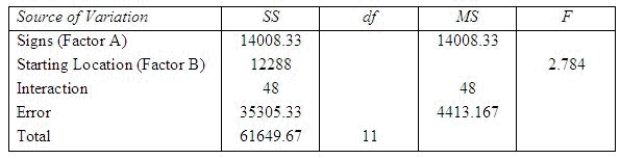 The degrees of freedom for the different building signs are ______________.
The degrees of freedom for the different starting location are ______________.
The degrees of freedom for the interaction between the levels of signs and starting location are ______________.
The error degrees of freedom are ______________.
The mean squares value for starting location is ______________.
The F test statistic for testing the main effect of types of signs is ______________.
The F test statistic for testing the interaction effect between the types of signs and the starting location is ______________.
In order to determine the critical value of the F ratio against which to test for differences between the levels of factor A, we should use numerator df = ______________, and denominator df = ______________.
In order to determine the critical value of the F ratio against which to test for differences between the levels of factor B, we should use numerator df = ______________, and denominator df = ______________.
In order to determine the critical value of the F ratio against which to test for interaction between levels of Factor A and levels of Factor B, we should use numerator df = ______________, and denominator of F = ______________.
The degrees of freedom for the different building signs are ______________.
The degrees of freedom for the different starting location are ______________.
The degrees of freedom for the interaction between the levels of signs and starting location are ______________.
The error degrees of freedom are ______________.
The mean squares value for starting location is ______________.
The F test statistic for testing the main effect of types of signs is ______________.
The F test statistic for testing the interaction effect between the types of signs and the starting location is ______________.
In order to determine the critical value of the F ratio against which to test for differences between the levels of factor A, we should use numerator df = ______________, and denominator df = ______________.
In order to determine the critical value of the F ratio against which to test for differences between the levels of factor B, we should use numerator df = ______________, and denominator df = ______________.
In order to determine the critical value of the F ratio against which to test for interaction between levels of Factor A and levels of Factor B, we should use numerator df = ______________, and denominator of F = ______________.
(Short Answer)
4.8/5  (32)
(32)
Analysis of variance (ANOVA) is a procedure for comparing more than two population means.
(True/False)
4.9/5  (35)
(35)
Showing 21 - 40 of 156
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)