Exam 11: The Analysis of Variance
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
In a two-way factor ANOVA with replications, the null hypothesis for testing whether interaction exists is that no interaction exists, while the alternative hypothesis is that interaction does exist.
(True/False)
4.8/5  (35)
(35)
Which of the following is not a required condition for one-way ANOVA?
(Multiple Choice)
4.8/5  (41)
(41)
The numerator or MST degrees of freedom are 3 and the denominator or MSE degrees of freedom are 18. The total number of observations in the completely randomized design must equal 20.
(True/False)
4.9/5  (23)
(23)
One-way ANOVA is applied to three independent samples having means 10, 13, and 18, respectively. If each observation in the third sample were increased by 30, the value of the F-statistics would:
(Multiple Choice)
4.8/5  (40)
(40)
The analysis of variance is a procedure that allows statisticians to compare two or more population:
(Multiple Choice)
4.7/5  (39)
(39)
Which of the following correctly describes the F statistic for the completely randomized design?
(Multiple Choice)
4.9/5  (37)
(37)
Based on public demand, price for seeds, and average yield, a farmer must choose which variety of wheat to grow. In the first step toward making a decision, the farmer planted eight test plots each with three varieties of wheat. The recorded yields (in pounds per plot) were used in an analysis of variance.  Use the output from the analysis of variance to test the null hypothesis of no difference among the mean yields of the three varieties of wheat. Use
Use the output from the analysis of variance to test the null hypothesis of no difference among the mean yields of the three varieties of wheat. Use 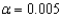 to draw conclusions.
Test statistic F = ______________
The rejection region is ______________.
______________
The sample in this problem ______________ that the mean yields for the three varieties are not the same.
to draw conclusions.
Test statistic F = ______________
The rejection region is ______________.
______________
The sample in this problem ______________ that the mean yields for the three varieties are not the same.
(Short Answer)
4.8/5  (37)
(37)
When the problem objective is to compare more than two populations, the experimental design that is the counterpart of the matched pairs experiment is called the randomized block design.
(True/False)
4.9/5  (42)
(42)
In a two-way ANOVA, where a is the number of factor A levels and b is the number of factor B levels, the number of the degrees of freedom for the "error term" is:
(Multiple Choice)
4.9/5  (32)
(32)
Tukey's method for paired comparisons assumes that the sample means are equal and independent of each other.
(True/False)
4.9/5  (34)
(34)
The following statistics were calculated based on samples drawn from three normal populations: 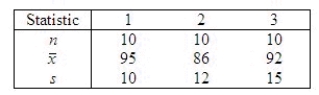 Set up the ANOVA table and test at the 5% level of significance to determine whether differences exist among the population means.
Test statistic = ______________
Critical Value(s) = ______________
Conclusion: ______________
Interpretation:
Differences ______________ exist among the population means.
Set up the ANOVA table and test at the 5% level of significance to determine whether differences exist among the population means.
Test statistic = ______________
Critical Value(s) = ______________
Conclusion: ______________
Interpretation:
Differences ______________ exist among the population means.
(Short Answer)
4.8/5  (37)
(37)
An avid runner was interested in whether there is a significant difference in the average wear (measured in weeks of use) among three brands of running shoes. To answer the question, the runner randomly selected six runners and assigned them to wear each of the three brands of running shoes until the shoes wore out. Each of the runners wore the brands of shoes in a random order. After the data had been recorded, the following output was generated using Minitab: 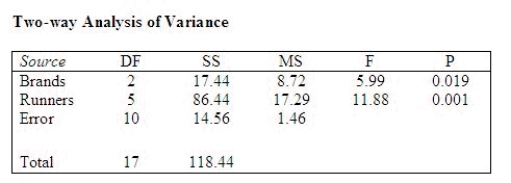 What are the blocks?
______________
What are the treatments?
______________
The p-value ______________ indicate significant results.
Is blocking necessary in this problem?
______________
Justify your answer.
________________________________________________________
Use the p-value approach to determine whether there is a significant difference in the average wear between the three brands of running shoes. Let
What are the blocks?
______________
What are the treatments?
______________
The p-value ______________ indicate significant results.
Is blocking necessary in this problem?
______________
Justify your answer.
________________________________________________________
Use the p-value approach to determine whether there is a significant difference in the average wear between the three brands of running shoes. Let 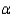 = 0.05.
The p-value ______________ indicate significant results.
______________ of the brands of running shoes has a significantly different average wear than the others.
= 0.05.
The p-value ______________ indicate significant results.
______________ of the brands of running shoes has a significantly different average wear than the others.
(Short Answer)
4.9/5  (44)
(44)
In the randomized block design for ANOVA where k is the number of treatments and b in the number of blocks, the degrees of freedom for error is given by:
(Multiple Choice)
4.7/5  (36)
(36)
A complete 3 x 2 factorial experiment is called balanced if:
(Multiple Choice)
4.8/5  (40)
(40)
A company conducted an experiment to determine the effect of two types of incentive pay plans on worker productivity for workers of two shifts. The company used an equal number of production workers from each of the two shifts and one-half of these workers were assigned to each plan. Then five workers from each pay plan-shift combination were selected and their productivity (in number of items produced) recorded for a one week period. The following output was generated using Minitab: 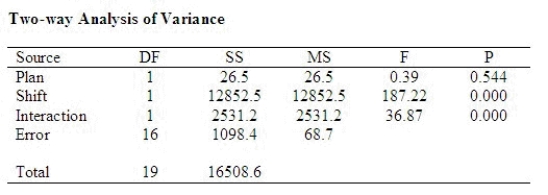 Is there significant interaction present in this problem? Let
Is there significant interaction present in this problem? Let 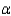 = 0.05.
The p-value ______________ indicate significant interaction.
Based on the previous answer, is testing for the main effects, plan and shift, appropriate?
________________________________________________________
= 0.05.
The p-value ______________ indicate significant interaction.
Based on the previous answer, is testing for the main effects, plan and shift, appropriate?
________________________________________________________
(Essay)
4.9/5  (34)
(34)
For which of the following departures from the conditions required for a completely randomized design is the procedure not considered robust?
(Multiple Choice)
4.8/5  (39)
(39)
In a one-way ANOVA, the following null and alternative hypotheses are appropriate: . 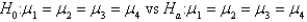
(True/False)
4.9/5  (37)
(37)
A textile company is interested in knowing if there is a difference in the breaking strength of four different kinds of thread. 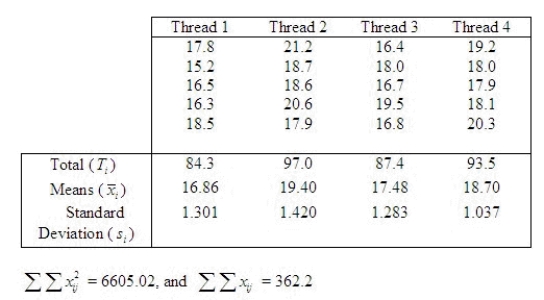 Test whether there is a significant difference in mean breaking strength of the four kinds of thread. Calculate the test statistic.
F = ______________
Set up the rejection region for
Test whether there is a significant difference in mean breaking strength of the four kinds of thread. Calculate the test statistic.
F = ______________
Set up the rejection region for 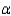 = 0.05.
The rejection region is ______________.
What conclusion can be drawn?
______________
______________ of the mean breaking strengths of the four kinds of threads is significantly different from the others.
Find the approximate p-value.
CI = ______________ Enter (n1, n2)
Find a 90% confidence interval for
= 0.05.
The rejection region is ______________.
What conclusion can be drawn?
______________
______________ of the mean breaking strengths of the four kinds of threads is significantly different from the others.
Find the approximate p-value.
CI = ______________ Enter (n1, n2)
Find a 90% confidence interval for 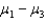 .
CI = ______________ Enter (n1, n2)
.
CI = ______________ Enter (n1, n2)
(Short Answer)
4.9/5  (42)
(42)
Showing 81 - 100 of 156
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)