Exam 7: Sampling Distributions
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
The sampling distribution of the sample mean 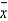 is the distribution of all possible sample means that could be computed from all possible sample of a given size n.
is the distribution of all possible sample means that could be computed from all possible sample of a given size n.
(True/False)
4.7/5  (32)
(32)
The mean of the sampling distribution of the sample proportion 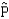 when n = 100 and p = 0.5 is 5.0.
when n = 100 and p = 0.5 is 5.0.
(True/False)
4.8/5  (32)
(32)
If all possible samples of size n are drawn from a large population with a mean of 20 and a standard deviation of 5, then the standard error of the sample mean equals 1.0 only for samples of size:
(Multiple Choice)
4.8/5  (41)
(41)
If a population standard deviation is equal to 24.8, then the sampling distribution of the sample mean 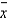 will have a standard deviation that is less than 24.8 for all possible sample sizes.
will have a standard deviation that is less than 24.8 for all possible sample sizes.
(True/False)
4.8/5  (35)
(35)
On a particular freeway in Michigan, it is reported that the proportion of cars that exceed the speed limit is 0.15. Given this information, the probability that a sample of 250 cars will have a sample proportion below 0.12 is approximately .0918.
(True/False)
4.8/5  (32)
(32)
The cause of a change in a process variable being monitored is regarded as random variation if it can be found and corrected.
(True/False)
4.7/5  (26)
(26)
The proportion of individuals with an Rh-positive blood type is 88%. You have a random sample of n = 500 individuals.
What is the mean of 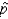 , the sample proportion with Rh-positive blood type?
______________
What is the standard deviation?
______________
Is the distribution approximately normal?
______________
What is the probability that the sample proportion exceeds 85%.
______________
What is the probability that the sample proportion
, the sample proportion with Rh-positive blood type?
______________
What is the standard deviation?
______________
Is the distribution approximately normal?
______________
What is the probability that the sample proportion exceeds 85%.
______________
What is the probability that the sample proportion 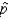 lies between 86% and 91%?
______________
99% of the time, the sample proportion
lies between 86% and 91%?
______________
99% of the time, the sample proportion 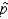 would lie between what two limits?
Lower Limit = ______________
Upper Limit = ______________
would lie between what two limits?
Lower Limit = ______________
Upper Limit = ______________
(Short Answer)
4.8/5  (23)
(23)
The sampling distribution of the sample mean is exactly normally distributed, regardless of the sample size n.
(True/False)
4.8/5  (19)
(19)
Given a population variance of 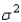 = 36 and a sample size of n = 9, these imply a standard deviation of the sampling distribution of the sample mean,
= 36 and a sample size of n = 9, these imply a standard deviation of the sampling distribution of the sample mean, 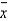 , of:
, of:
(Multiple Choice)
4.9/5  (36)
(36)
For a 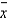 control chart, the lower and upper control limits are usually set at:
control chart, the lower and upper control limits are usually set at:
(Multiple Choice)
4.8/5  (32)
(32)
The amount of time to complete a particular exam is believed to have a mean of 52 minutes and a standard deviation of 4.8 minutes. A sample of 36 students was selected and their times to finish the exam recorded.
Is the sampling distribution of the sample mean approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
What is the probability this sample produces an average of less than 50 minutes?
______________
If the sample mean 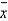 is actually 50 minutes, is it likely that
is actually 50 minutes, is it likely that 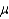 = 52?
______________
Explain.
________________________________________________________
= 52?
______________
Explain.
________________________________________________________
(Essay)
4.7/5  (37)
(37)
The mean of the sample means and the standard deviation of 50 samples of size 5 taken from a production process under control are found to be 300 and 25, respectively. The lower control limit for the 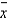 chart is located at:
chart is located at:
(Multiple Choice)
4.8/5  (36)
(36)
Assume that the proportion of defective items in a sample of 400 items is 0.20.
Is the normal approximation to the sampling distribution of 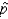 appropriate in this situation?
______________
Find the probability that
appropriate in this situation?
______________
Find the probability that 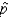 is greater than 0.23.
______________
Find the probability that
is greater than 0.23.
______________
Find the probability that 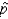 lies between 0.16 and 0.24.
______________
lies between 0.16 and 0.24.
______________
(Short Answer)
4.7/5  (33)
(33)
A candy bar factory is pouring chocolate into molds to cool. The finished bars are sold as 1.25 ounce bars. The company will lose money if the molds are over-filled. If the molds are under-filled, the weight of the candy bars will be less than the wrapper label says, and the Food and Drug Administration will fine the company for misrepresenting the size of its product. The company wants to create an 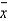 chart to monitor the weight of the candy bars. Suppose there are 5 samples of size 30 each taken, and their sample means are 1.27, 1.22, 1.26, 1.23, and 1.26 ounces.
What is the centerline value?
______________
The calculated value of s, the sample standard deviation of all nk = (30)(5) = 150 observations, is 0.12 ounces. What is the standard error of the mean of 30 observations?
______________
What are the control limits?
UCL = ______________
LCL = ______________
How is the
chart to monitor the weight of the candy bars. Suppose there are 5 samples of size 30 each taken, and their sample means are 1.27, 1.22, 1.26, 1.23, and 1.26 ounces.
What is the centerline value?
______________
The calculated value of s, the sample standard deviation of all nk = (30)(5) = 150 observations, is 0.12 ounces. What is the standard error of the mean of 30 observations?
______________
What are the control limits?
UCL = ______________
LCL = ______________
How is the 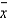 chart used in this situation?
________________________________________________________
chart used in this situation?
________________________________________________________
(Essay)
4.9/5  (32)
(32)
Random samples of size 36 each are taken from a large population whose mean is 120 and standard deviation is 39. The mean and standard error of the sampling distribution of sample mean, respectively, are:
(Multiple Choice)
4.7/5  (29)
(29)
Given a population proportion of p = .8 and a sample size of n = 100, these imply a standard deviation of the sampling distribution of the sample proportion 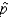 of:
of:
(Multiple Choice)
4.7/5  (29)
(29)
If a process is in control, we expect all the data values to fall within three standard deviations of the mean.
(True/False)
4.7/5  (39)
(39)
A summary measure calculated for a population is called a parameter and is designated by Greek letters (such as 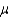 for mean or
for mean or 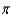 for proportion).
for proportion).
(True/False)
4.9/5  (35)
(35)
Showing 21 - 40 of 162
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)