Exam 4: Probability and Probability Distributions

A box contains one red, three blue and two green marbles. Two marbles are randomly selected without replacement. Let R = {The selected marble is red.} B = {The selected marble is blue.} G = {The selected marble is green.} C = {Both marbles selected are the same color.} D = {At least one of the marbles is blue.} a. Find P(C). b. Find P(D). c. Find $A box contains one red, three blue and two green marbles. Two marbles are randomly selected without replacement. Let R = {The selected marble is red.} B = {The selected marble is blue.} G = {The selected marble is green.} C = {Both marbles selected are the same color.} D = {At least one of the marbles is blue.} a. Find P(C). b. Find P(D). c. Find 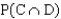. d. Find . e. Find P(D | C). $ . d. Find $A box contains one red, three blue and two green marbles. Two marbles are randomly selected without replacement. Let R = {The selected marble is red.} B = {The selected marble is blue.} G = {The selected marble is green.} C = {Both marbles selected are the same color.} D = {At least one of the marbles is blue.} a. Find P(C). b. Find P(D). c. Find . d. Find 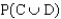. e. Find P(D | C). $ . e. Find P(D | C). __

(Short Answer)

4.8/5

(32)

Question 81

In general, there is no difference between the simple events and the events.

(True/False)

4.7/5

(30)

Question 82

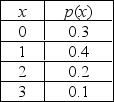The random variable x is defined as the number of mistakes made by a typist on a randomly chosen page of a physics thesis. The probability distribution follows. $The random variable x is defined as the number of mistakes made by a typist on a randomly chosen page of a physics thesis. The probability distribution follows. Round your answer to four decimal places, if necessary. a. What is E(x)? b. Find . c. Find P(x < 1). d. Find . e. In what fraction of pages in the thesis would the number of mistakes made be within two standard deviations of the mean? $ Round your answer to four decimal places, if necessary. a. What is E(x)? b. 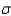Find $The random variable x is defined as the number of mistakes made by a typist on a randomly chosen page of a physics thesis. The probability distribution follows. Round your answer to four decimal places, if necessary. a. What is E(x)? b. Find . c. Find P(x < 1). d. Find . e. In what fraction of pages in the thesis would the number of mistakes made be within two standard deviations of the mean? $ . c. Find P(x < 1). d. Find $The random variable x is defined as the number of mistakes made by a typist on a randomly chosen page of a physics thesis. The probability distribution follows. Round your answer to four decimal places, if necessary. a. What is E(x)? b. Find . c. Find P(x < 1). d. Find 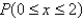. e. In what fraction of pages in the thesis would the number of mistakes made be within two standard deviations of the mean? $ . e. In what fraction of pages in the thesis would the number of mistakes made be within two standard deviations of the mean?

(Short Answer)

4.8/5

(23)

Question 83

A table, formula, or graph that shows all possible values x a random variable can assume, together with their associated probabilities P(x) is called:

(Multiple Choice)

4.9/5

(29)

Question 84

The probability distribution of the number of accidents in Grand Rapids, Michigan, each day is given by Based on this distribution, the standard deviation of the number of accidents per day is approximately: Round your answer to two decimal places.

(Multiple Choice)

4.8/5

(33)

Question 85

Two events A and B are said to mutually exclusive if P(A B) = 0.

(True/False)

4.8/5

(23)

Question 86

A sample space S consists of five simple events with these probabilities: 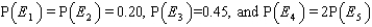a. Find the probability for simple event E₄. b. Find the probabilities for these two events: A: E₁, E₃, E₄ c. B: E₂, E₄ d. List the simple events that are either in event A or event B or both: e. List the simple events that are in both event A and event B: __

(Short Answer)

4.8/5

(34)

Question 87

A student has decided to study at a local coffee shop. After some time, she gets hungry. There are two beverages available: tea and coffee and three bakery items: donuts, muffins and bagels. Define the following events: C = {student gets coffee to drink} T = {student gets tea to drink} D = {student gets a donut to eat} M = {student gets a muffin to eat} B = {student gets a bagel to eat} a. She decides she wants to get one item to eat and one item to drink. List the elements in the sample space S. ______________ b. If each combination is equally likely, what is the probability the student gets coffee and a bagel? c. If each combination is equally likely, what is the probability the student gets a muffin and coffee or tea? d. If each combination is equally likely, what is the probability the student does not get a donut?

(Short Answer)

4.9/5

(36)

Question 88

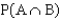Suppose that P(A) = 0.4, P(B) = 0.5, and that events A and B are mutually exclusive. a. Find . b. Find .

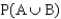(Short Answer)

4.7/5

(35)

Question 89

Suppose A and B are mutually exclusive events where P(A) = 0.2 and P(B) = 0.3. Then P(A 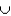B) = 0.5.

(True/False)

4.9/5

(43)

Question 90

If P(A) = 0, P(B) = 0.4, and P(A B) = 0, then events A and B are independent.

(True/False)

4.8/5

(48)

Question 91

A laboratory test for a disease affecting 5% of the population is either positive, indicating the disease is present, or negative, indicating the disease is not present. When people having the disease are tested, 80% of the tests come back positive, and when people who don't have the disease are tested, 15% of the tests come back from the lab marked positive (a false positive result). What is the chance a randomly chosen person's test results would come back positive? ______________

(Short Answer)

4.9/5

(23)

Question 92

In the "Quick Draw" casino card game, a player chooses one card from a deck of 52 well-shuffled cards. If the card the player selects is the king of hearts, the player wins $104; if the card is an ace, the player wins $78; if the card selected is anything else, the player loses $13. Considering a negative amount won to be a loss, how much should the player expect to win in one play of "Quick Draw"? $ ______________

(Short Answer)

4.9/5

(41)

Question 93

If P(A) = 0.4, P(B) = 0.5, and P(A B) = 0.7, then P(A B) = 0.2.

(True/False)

4.9/5

(43)

Question 94

A random variable is any variable the numerical value of which is determined by a random experiment, and, thus, by chance.

(True/False)

4.8/5

(44)

Question 95

The probability of an event and the probability of its complement always sum to:

(Multiple Choice)

4.7/5

(34)

Question 96

The probability distribution of your winnings at a casino's card game is shown below. 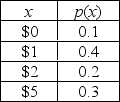a. What is the chance you win more than $1 if you play just once? b. How much should you expect to win if you play the game once? c. After breaking the bank at the casino playing this card game, you decide to open your own casino where the customers can play your favorite card game. How much should you charge the players if you want to have an average profit of $1 per play? __

(Short Answer)

4.9/5

(38)

Question 97

If events A and B are mutually exclusive, then the probability of both events occurring simultaneously is equal to:

(Multiple Choice)

4.9/5

(26)

Question 98

A political scientist asked a group of people how they felt about two political policy statements. Each person was to respond A (agree), N (neutral), or D (disagree) to each policy statement. a. Describe the sample space; that is, list all possible response combinations to the two statements. ____________________________ b. Assuming each response combination in part (a) is equally likely, what is the probability the person being interviewed agrees with at least one of the two policy statements? c. Assuming each response combination in part (a) is equally likely, what is the probability the person being interviewed agrees with exactly one of the two political policy statements? d.Assuming each response combination in part (a) is equally likely, what is the probability the person being interviewed agrees with the two political policy statements?

(Short Answer)

4.9/5

(34)

Question 99

Approximately 5% of the bolts coming off a production line have serious defects. Two bolts are randomly selected for inspection. Find the probability distribution for x, the number of defective bolts in the sample. a. P(x = 0) = P(both bolts are not defective) b. P(x = 1) = P(one bolt is defective) c. P(x = 2) = P(both bolts are defective) d. Find E(x). e. Find . __

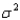(Short Answer)

4.8/5

(36)

Question 100

Showing 81 - 100 of 136

In general, there is no difference between the simple events and the events.

A table, formula, or graph that shows all possible values x a random variable can assume, together with their associated probabilities P(x) is called:

The probability distribution of the number of accidents in Grand Rapids, Michigan, each day is given by Based on this distribution, the standard deviation of the number of accidents per day is approximately: Round your answer to two decimal places.

Two events A and B are said to mutually exclusive if P(A B) = 0.

Suppose that P(A) = 0.4, P(B) = 0.5, and that events A and B are mutually exclusive. a. Find . b. Find .

Suppose A and B are mutually exclusive events where P(A) = 0.2 and P(B) = 0.3. Then P(A B) = 0.5.

If P(A) = 0, P(B) = 0.4, and P(A B) = 0, then events A and B are independent.

If P(A) = 0.4, P(B) = 0.5, and P(A B) = 0.7, then P(A B) = 0.2.

A random variable is any variable the numerical value of which is determined by a random experiment, and, thus, by chance.

The probability of an event and the probability of its complement always sum to:

If events A and B are mutually exclusive, then the probability of both events occurring simultaneously is equal to:

Describing Data With Graphs

Describing Data With Numerical Measures

Describing Bivariate Data

Several Useful Discrete Distributions

The Normal Probability Distribution

Sampling Distributions

Large-Sample Estimation

Large-Sample Tests of Hypotheses

Inference From Small Samples

The Analysis of Variance

Linear Regression and Correlation

Multiple Regression Analysis

Analysis of Categorical Data

Nonparametric Statistics

Filters

Exam 4: Probability and Probability Distributions

In general, there is no difference between the simple events and the events.

A table, formula, or graph that shows all possible values x a random variable can assume, together with their associated probabilities P(x) is called:

The probability distribution of the number of accidents in Grand Rapids, Michigan, each day is given by Based on this distribution, the standard deviation of the number of accidents per day is approximately: Round your answer to two decimal places.

Two events A and B are said to mutually exclusive if P(A B) = 0.

Suppose that P(A) = 0.4, P(B) = 0.5, and that events A and B are mutually exclusive. a. Find . ______________ b. Find . ______________

Suppose A and B are mutually exclusive events where P(A) = 0.2 and P(B) = 0.3. Then P(A B) = 0.5.

If P(A) = 0, P(B) = 0.4, and P(A B) = 0, then events A and B are independent.

If P(A) = 0.4, P(B) = 0.5, and P(A B) = 0.7, then P(A B) = 0.2.

A random variable is any variable the numerical value of which is determined by a random experiment, and, thus, by chance.

The probability of an event and the probability of its complement always sum to:

If events A and B are mutually exclusive, then the probability of both events occurring simultaneously is equal to:

Describing Data With Graphs

Describing Data With Numerical Measures

Describing Bivariate Data

Several Useful Discrete Distributions

The Normal Probability Distribution

Sampling Distributions

Large-Sample Estimation

Large-Sample Tests of Hypotheses

Inference From Small Samples

The Analysis of Variance

Linear Regression and Correlation

Multiple Regression Analysis

Analysis of Categorical Data

Nonparametric Statistics

Filters

Suppose that P(A) = 0.4, P(B) = 0.5, and that events A and B are mutually exclusive. a. Find . b. Find .