Exam 4: Extrema on an Interval
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Suppose a manufacturer has determined that the total cost C of operating a factory is where is the number of units produced. At what level of production will the average cost per unit be minimized? (The average cost per unit is .)
(Multiple Choice)
4.7/5  (31)
(31)
interval . If Rolle's Theorem can be applied, find all values of in the open interval such that
(Multiple Choice)
4.8/5  (32)
(32)
Locate any relative extrema and inflection points of the function . Use a graphing utility to confirm your results.
(Multiple Choice)
4.7/5  (31)
(31)
(a)Find the critical numbers of (if any);
(b) Find the open intervals where the function is increasing or decreasing; and
(c) Apply the First Derivative Test to identify all relative extrema. Then use a graphing utility to confirm your results.
(Multiple Choice)
4.7/5  (28)
(28)
Determine the x-coordinate(s) of any relative extrema and inflection points of the function
(Multiple Choice)
4.8/5  (28)
(28)
Find the points of inflection and discuss the concavity of the function on the interval
(Multiple Choice)
4.8/5  (25)
(25)
Find the length and width of a rectangle that has an area of 968 square feet and whose perimeter is a minimum.
(Multiple Choice)
4.9/5  (29)
(29)
A plane begins its takeoff at 2:00 P.M. on a 2200-mile flight. After 12.5 hours, the plane arrives at its destination. Explain why there are at least two times during the flight when the
Speed of the plane is 100 miles per hour.
(Multiple Choice)
4.9/5  (43)
(43)
Match the function , use a graphing utility to complete the table and estimate the limit as x approaches infinity. x 1 1 1 1 1 1 1 f(x)
(Multiple Choice)
5.0/5  (37)
(37)
Norman window is constructed by adjoining a semicircle to the top of an ordinary rectangular window (see figure). Find the dimensions of a Norman window of maximum area if the Total perimeter is 38 feet.
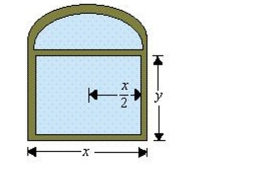
(Multiple Choice)
4.8/5  (36)
(36)
Find the point on the graph of the function that is closest to the point . Round all numerical values in your answer to four decimal places.
(Multiple Choice)
4.9/5  (34)
(34)
coefficients are real numbers, which satisfies the conditions given below.
Relative maximum:
Relative minimum:
Inflection point:
(Multiple Choice)
4.7/5  (30)
(30)
A rectangle is bounded by the x- and y-axes and the graph of figure). What length and width should the rectangle have so that its area is a maximum?
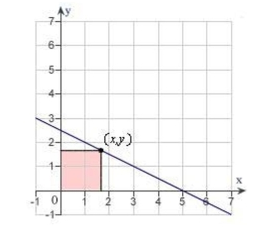
(Multiple Choice)
4.9/5  (37)
(37)
intervals on which the function is increasing or decreasing.
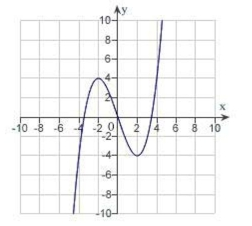
(Multiple Choice)
4.7/5  (37)
(37)
Showing 81 - 100 of 147
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)