Exam 4: Extrema on an Interval
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Find the points of inflection and discuss the concavity of the function.
(Multiple Choice)
4.9/5  (35)
(35)
Identify the open intervals where the function
is increasing or decreasing.
(Multiple Choice)
4.9/5  (38)
(38)
Find all relative extrema of the function . Use the Second Derivative Test where applicable.
(Multiple Choice)
4.9/5  (44)
(44)
Determine the open intervals on which the graph of is concave downward or concave upward.
(Multiple Choice)
4.7/5  (36)
(36)
Find measurements of the base and altitude of a triangle are found to be 54 and 33 centimeters. The possible error in each measurement is 0.25 centimeter. Use differentials to estimate The propagated error in computing the area of the triangle. Round your answer to four decimal places.
(Multiple Choice)
4.9/5  (29)
(29)
The graph of a function f is is shown below. Sketch the graph of the derivative . 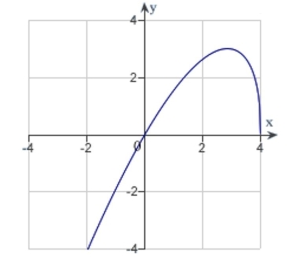
(Multiple Choice)
4.8/5  (29)
(29)
The height of an object t seconds after it is dropped from a height of 250 meters is . Find the time during the first 8 seconds of fall at which the instantaneous velocity equals the average velocity.
(Multiple Choice)
5.0/5  (36)
(36)
Find all relative extrema of the function . Use the Second Derivative Test where applicable.
(Multiple Choice)
4.8/5  (30)
(30)
A ball bearing is placed on an inclined plane and begins to roll. The angle of elevation of the plane is radians. The distance (in meters) the ball bearing rolls in seconds is Determine the speed of the ball bearing after seconds.
(Multiple Choice)
4.9/5  (35)
(35)
Sketch the graph of the function using any extrema, intercepts, symmetry, and asymptotes.
(Multiple Choice)
4.9/5  (31)
(31)
Find the point of inflection of the graph of the function on the interval
(Multiple Choice)
4.9/5  (37)
(37)
Determine whether the Mean Value Theorem can be applied to the function on the closed interval . If the Mean Value Theorem can be applied, find all numbers in the open interval such that .
(Multiple Choice)
4.8/5  (44)
(44)
Sketch a graph of f is shown below. For which values of x is 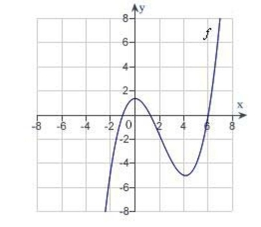
(Multiple Choice)
4.8/5  (38)
(38)
A container holds 3 liters of a 25% brine solution. A model for the concentration C of the mixture after adding x liters of a 0.67 % brine solution to the container and then draining x liters
Of the well-mixed solution is given as places.
(Multiple Choice)
4.8/5  (32)
(32)
interval Round numerical values in your answer to three decimal places.
(Multiple Choice)
4.7/5  (27)
(27)
Showing 121 - 140 of 147
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)