Exam 4: Extrema on an Interval
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
A company introduces a new product for which the number of units sold S is where is the time in months since the product was introduced. Find the average value of during the first year.
(Multiple Choice)
4.8/5  (26)
(26)
Determine whether Rolle's Theorem can be applied to the function on the closed interval . If Rolle's Theorem can be applied, find all numbers in the open interval such that .
(Multiple Choice)
4.9/5  (44)
(44)
Find two positive numbers whose product is 181 and whose sum is a minimum.
(Multiple Choice)
4.9/5  (34)
(34)
The resistance R of a certain type of resistor is where R is measured in ohms and the temperature T is measured in degrees Celsius. Use a computer algebra System to find
(Multiple Choice)
4.9/5  (41)
(41)
Determine whether the Mean Value Theorem can be applied to the function on the closed interval . If the Mean Value Theorem can be applied, find all numbers in the open interval such that .
(Multiple Choice)
4.7/5  (51)
(51)
A meteorologist measures the atmospheric pressure P (in kilograms per square meter) at altitude h (in kilometers). The data are shown below. Find the rate of change of the pressure with Respect to altitude one decimal place. h 0 5 10 15 20 p 28,085 15,169 6,458 3,371 1405
(Multiple Choice)
4.8/5  (47)
(47)
Analyze the graph of the function relative extrema, points of inflection and asymptotes. Also determine where the graph is increasing or decreasing and concave up or concave down. Then identify the graph from the choices below.
(Multiple Choice)
4.8/5  (40)
(40)
A company introduces a new product for which the number of units sold S is where is the time in months since the product was introduced. During what month does equal the average value of during the first year?
(Multiple Choice)
4.7/5  (27)
(27)
the First Derivative Test. Round numerical values in your answer to three decimal places.
(Multiple Choice)
4.9/5  (29)
(29)
Find the relative minima of the First Derivative Test. Round numerical values in your answer to three decimal places.
(Multiple Choice)
4.8/5  (39)
(39)
The graph of a function f is is shown below. Sketch the graph of the derivative
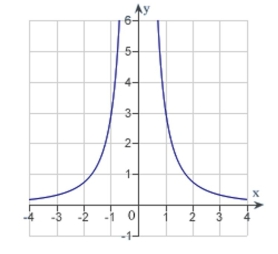
(Multiple Choice)
4.9/5  (37)
(37)
The vsum of the perimeters of an equilateral triangle and a square is 19. Find the dimensions of the triangle and the square that produce a minimum total area.
(Multiple Choice)
4.9/5  (36)
(36)
Showing 101 - 120 of 147
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)