Exam 17: Vector Calculus
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Find 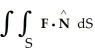 , where F(x, y, z) = x
, where F(x, y, z) = x 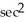 y i +
y i + 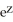 ln x j - z
ln x j - z 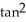 y k, S is the sphere of radius 3 centred at the origin, and
y k, S is the sphere of radius 3 centred at the origin, and  is the unit outward normal field on S.
is the unit outward normal field on S.
(Multiple Choice)
4.8/5  (52)
(52)
Calculate the surface integral 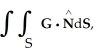 where G = (x + y) i + (y + z) j + (z + x) k and S is the sphere
where G = (x + y) i + (y + z) j + (z + x) k and S is the sphere 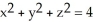 with outward normal.
with outward normal.
(Multiple Choice)
5.0/5  (41)
(41)
Use Green's Theorem to evaluate the line integral 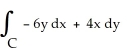 counterclockwise around the square with vertices (0, 3), (3, 0), (-3, 0), and (0, -3).
counterclockwise around the square with vertices (0, 3), (3, 0), (-3, 0), and (0, -3).
(Multiple Choice)
4.9/5  (31)
(31)
Let F = -y i + x j + z k. Use Stokes's Theorem to find the flux of upward through the paraboloid ![Let F = -y i + x j + z k. Use Stokes's Theorem to find the flux of \textbf{ curl F} upward through the paraboloid where u [0, 1] and v [0, 2 \pi ].](https://storage.examlex.com/TB9661/11ee77e1_7799_f746_a0f8_0b4a15d2df4c_TB9661_11.jpg) where u
where u ![Let F = -y i + x j + z k. Use Stokes's Theorem to find the flux of \textbf{ curl F} upward through the paraboloid where u [0, 1] and v [0, 2 \pi ].](https://storage.examlex.com/TB9661/11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11.jpg) [0, 1] and v 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [0, 2 ].
[0, 1] and v 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [0, 2 ].
(Multiple Choice)
4.7/5  (38)
(38)
Find the acute angle (to the nearest degree) between the normals of the paraboloid z = x2 + y2 - 6 and the sphere x2 + y2 + z2 = 26 at the point (-3, 1, 4) on both surfaces.
(Short Answer)
4.9/5  (38)
(38)
Evaluate the line integral 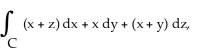 where C is the circle given by the parametric equations
where C is the circle given by the parametric equations 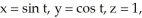 for
for 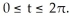
(Multiple Choice)
4.8/5  (39)
(39)
Find the outward flux of F = ln( 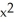 +
+ 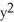 ) i -
) i - 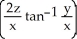 j + z
j + z 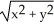 k across the boundary of the region
k across the boundary of the region 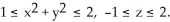
(Multiple Choice)
4.8/5  (39)
(39)
Evaluate 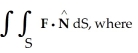 F = x
F = x 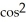 y i + xz j + z
y i + xz j + z 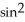 y k and S is the sphere of radius 3 with centre at the origin and unit outward normal field
y k and S is the sphere of radius 3 with centre at the origin and unit outward normal field  .
.
(Multiple Choice)
4.7/5  (38)
(38)
Use Green's theorem in the plane to show that the area A of a regular plane region R enclosed by a positively oriented, piecewise smooth, simple closed curve C is given by A = 
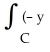 dx + x dy).
dx + x dy).
(Essay)
4.9/5  (33)
(33)
If the vector field H = f(r) r, r 0 is solenoidal, find an expression for f(r).
(Multiple Choice)
4.7/5  (38)
(38)
Let F = f(x, y, z) i + g(x, y, z) j + h(x, y, z) k be a vector field in 3-space whose components f, g, and h have continuous second partial derivatives. Calculate div curl F in terms of those partials.
(Multiple Choice)
4.9/5  (50)
(50)
Let C be a cone whose base is an arbitrarily shaped region in the plane z = h > 0 having area A, and whose vertex is at the origin. By calculating the flux of 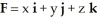 out of C through its entire surface both directly and by using the Divergence Theorem, find the volume of C.
out of C through its entire surface both directly and by using the Divergence Theorem, find the volume of C.
(Multiple Choice)
4.9/5  (33)
(33)
Compute the divergence for the vector field F = (xy + xz) i + (yz + yx) j + (zx + zy) k.
(Multiple Choice)
4.7/5  (42)
(42)
Show that there does not exist a twice continuously differentiable vector field G such that = x i + y j + z k.
(Essay)
4.9/5  (44)
(44)
Let 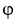 = arctan(x) - arctan(z) and
= arctan(x) - arctan(z) and 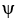 =
= 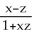 . Find a simplified expression for (11ee7bac_4a3a_9aaa_ae82_759e3f104991_TB9661_11 ) × (11ee7bac_77f1_7c2b_ae82_019616e1397c_TB9661_11 ) .
. Find a simplified expression for (11ee7bac_4a3a_9aaa_ae82_759e3f104991_TB9661_11 ) × (11ee7bac_77f1_7c2b_ae82_019616e1397c_TB9661_11 ) .
(Multiple Choice)
4.8/5  (31)
(31)
Showing 41 - 60 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)