Exam 17: Vector Calculus
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
The local bases in cylindrical coordinates (r , , z) are given by  = cos( ) i + sin( ) j ,
= cos( ) i + sin( ) j , 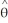 = - sin( ) i + cos( ) j, and
= - sin( ) i + cos( ) j, and  = k.
Express the acceleration a of a moving particle in space in terms of the local bases above.
= k.
Express the acceleration a of a moving particle in space in terms of the local bases above.
(Multiple Choice)
4.8/5  (39)
(39)
If 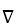 × F = 0 at every point of a simply connected open region D in 3-space, evaluate
× F = 0 at every point of a simply connected open region D in 3-space, evaluate 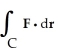 for any piecewise smooth closed curve in D.
for any piecewise smooth closed curve in D.
(Multiple Choice)
4.7/5  (46)
(46)
Evaluate the integral 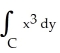 -
- 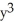 dx counterclockwise around the closed curve formed by y = x3 and y = x, between the points (0, 0) and (1, 1).
dx counterclockwise around the closed curve formed by y = x3 and y = x, between the points (0, 0) and (1, 1).
(Multiple Choice)
4.9/5  (43)
(43)
A certain region R in 3-space has volume 5 cubic units and centroid at the point (2, -3, 4). Find the flux of 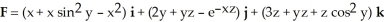 out of R across its boundary.
out of R across its boundary.
(Multiple Choice)
4.8/5  (31)
(31)
Use Green's Theorem to compute 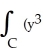 + xy) dx + (
+ xy) dx + ( 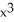 + xy) dy counterclockwise around the rectangle having vertices (± 1, 1) and (± 1, 2).
+ xy) dy counterclockwise around the rectangle having vertices (± 1, 1) and (± 1, 2).
(Multiple Choice)
4.9/5  (34)
(34)
Use the Divergence Theorem to evaluate the surface integral 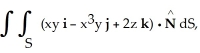 where S is the part of the cone
where S is the part of the cone 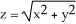 below z = 2, and
below z = 2, and 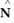 is the unit normal to S with positive z-component. (An additional surface must be introduced to enclose a volume.)
is the unit normal to S with positive z-component. (An additional surface must be introduced to enclose a volume.)
(Multiple Choice)
4.9/5  (37)
(37)
Let 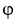 be a scalar field and F be a vector field, both assumed to be sufficiently smooth. Which of the following expressions is meaningless?
be a scalar field and F be a vector field, both assumed to be sufficiently smooth. Which of the following expressions is meaningless?
(Multiple Choice)
5.0/5  (48)
(48)
Find the flux of G = (x 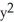 + 2zy) i + (y
+ 2zy) i + (y 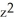 -
- 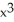 ) j +
) j + 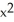 z k outward through the sphere
z k outward through the sphere 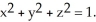
(Multiple Choice)
4.9/5  (31)
(31)
Find the flux of F = x i + 2y j out of the circular disk of radius 2 centred at (3, -5).
(Multiple Choice)
4.8/5  (36)
(36)
Let B be a constant vector and let G(r) = (B × r) × r be a vector potential of the solenoidal vector field F. Find F.
(Multiple Choice)
4.8/5  (42)
(42)
The local bases in cylindrical coordinates (r , , z) are given by  = cos( ) i + sin( ) j,
= cos( ) i + sin( ) j, 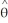 = - sin( ) i + cos( ) j, and
= - sin( ) i + cos( ) j, and  = k.Express the velocity v of a moving particle in space in terms of the local bases above.
= k.Express the velocity v of a moving particle in space in terms of the local bases above.
(Multiple Choice)
4.9/5  (32)
(32)
Calculate the curl of the vector field V = x sin y i + cos y j + xy k.
(Multiple Choice)
4.9/5  (34)
(34)
Evaluate the integral of 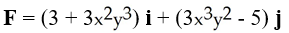 over the portion of the ellipse
over the portion of the ellipse 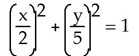 in the first quadrant, traversed in the counterclockwise direction.
in the first quadrant, traversed in the counterclockwise direction.
(Multiple Choice)
4.8/5  (38)
(38)
Evaluate the line integral 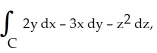 where C is the circle
where C is the circle 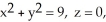 oriented clockwise as seen from high on the z-axis.
oriented clockwise as seen from high on the z-axis.
(Multiple Choice)
4.9/5  (39)
(39)
Use the Divergence Theorem to find the outward flux of F = 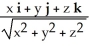 across the boundary of the region
across the boundary of the region 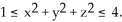
(Multiple Choice)
4.9/5  (29)
(29)
Let F = (z - y) i + (x - z) j + (y - x) k. Compute the work done by the force F in moving an object along the curve of intersection of the cylinder 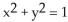 with the plane
with the plane 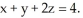 The orientation of the curve is consistent with the upward normal on the plane.
The orientation of the curve is consistent with the upward normal on the plane.
(Multiple Choice)
4.8/5  (32)
(32)
Use Green's Theorem to compute the integral 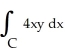 counterclockwise around the square with vertices at (4, 2), (4, 5), (7, 5), and (7, 2).
counterclockwise around the square with vertices at (4, 2), (4, 5), (7, 5), and (7, 2).
(Multiple Choice)
4.7/5  (37)
(37)
Showing 61 - 80 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)