Exam 17: Vector Calculus
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
If r = x i + y j + z k and k is a constant vector field in R3, then
(Multiple Choice)
4.9/5  (36)
(36)
Evaluate 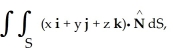 where S is the first-octant part of the sphere of radius a centred at the origin. (Hint: Even though S is not a closed surface, it is still easiest to use the Divergence Theorem because the integrand in the surface integral is zero on the coordinate planes.)
where S is the first-octant part of the sphere of radius a centred at the origin. (Hint: Even though S is not a closed surface, it is still easiest to use the Divergence Theorem because the integrand in the surface integral is zero on the coordinate planes.)
(Multiple Choice)
4.9/5  (28)
(28)
Let 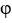 and F be sufficiently smooth scalar and vector fields, respectively.Express the well-known identity
and F be sufficiently smooth scalar and vector fields, respectively.Express the well-known identity 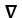 . (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F ) = (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 ) . F + 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11. F) using the notations grad , div or curl.
. (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F ) = (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 ) . F + 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11. F) using the notations grad , div or curl.
(Multiple Choice)
4.7/5  (32)
(32)
Let F = - 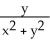 i +
i + 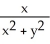 j and let C be the boundary of circle
j and let C be the boundary of circle 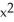 +
+ 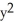 = 9 oriented counterclockwise. Use Green's Theorem to evaluate
= 9 oriented counterclockwise. Use Green's Theorem to evaluate 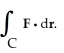
(Multiple Choice)
4.8/5  (32)
(32)
In cylindrical coordinates, find 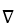 . F for F =
. F for F = 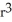
 + rz cos( )
+ rz cos( )  + rz sin( ) k.
+ rz sin( ) k.
(Multiple Choice)
4.8/5  (46)
(46)
Use Stokes's Theorem to evaluate the integral 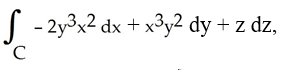 where C is the curve of intersection of the sphere
where C is the curve of intersection of the sphere 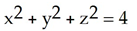 and the plane
and the plane 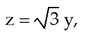 oriented counterclockwise as seen from high on the z-axis.
oriented counterclockwise as seen from high on the z-axis.
(Multiple Choice)
4.8/5  (42)
(42)
Let F be a smooth vector field in 3-space satisfying the condition 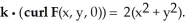 Find the flux of curl F upward through the part of the
Find the flux of curl F upward through the part of the 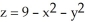 lying above the xy-plane.
lying above the xy-plane.
(Multiple Choice)
4.8/5  (35)
(35)
Use Stokes's Theorem to evaluate the line integral 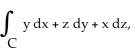 where C is the triangle with vertices (0, 0, 1), (0, 1, 1) and (1, 0, 0) with counterclockwise orientation as seen from high on the z-axis.
where C is the triangle with vertices (0, 0, 1), (0, 1, 1) and (1, 0, 0) with counterclockwise orientation as seen from high on the z-axis.
(Multiple Choice)
4.9/5  (37)
(37)
Use Green's theorem in the plane to find the x-coordinate of the centroid of a regular plane region R (with areaA) enclosed by a positively oriented, piecewise smooth, simple closed curve C .
(Multiple Choice)
4.9/5  (39)
(39)
If C is the positively oriented boundary of a plane region R having area 3 units and centroid at the point (12, 6), evaluate (i) 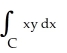 (ii)
(ii) 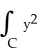 dx + 3xy dy
dx + 3xy dy
(Multiple Choice)
4.9/5  (35)
(35)
Find all values of the nonzero constant real numbers a, b, and c so that the vector field F = a cos( 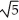 x + 2y )cosh (c z) i + b cos (
x + 2y )cosh (c z) i + b cos ( 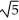 x + 2y)cosh (c z) j + c sin(
x + 2y)cosh (c z) j + c sin( 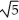 x + 2y)sinh(c z) k is both and .
x + 2y)sinh(c z) k is both and .
(Multiple Choice)
4.7/5  (45)
(45)
Using spherical polar coordinates, find 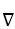 × F for F =
× F for F = 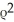 sin( )
sin( )  + sin( )
+ sin( ) 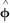 +
+ 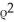 cos( )
cos( )  .
.
(Multiple Choice)
4.7/5  (35)
(35)
Evaluate the integral 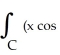 (
( 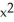 ) - 2y) dx + (3x - ysin(
) - 2y) dx + (3x - ysin( 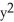 )) dy counterclockwise around the triangle in the xy-plane having vertices (0, 0), (2, 2), and (2, 0).
)) dy counterclockwise around the triangle in the xy-plane having vertices (0, 0), (2, 2), and (2, 0).
(Multiple Choice)
4.8/5  (39)
(39)
Find the flux of 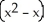 i - xy j +3z k out of the solid region bounded by the parabolic cylinder
i - xy j +3z k out of the solid region bounded by the parabolic cylinder 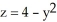 and the planes
and the planes 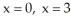 , and
, and 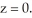
(Multiple Choice)
4.9/5  (32)
(32)
Use Green's Theorem to compute the integral 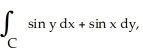 where C is the triangle formed by the lines y = -x + 1, x = 0 and y = 0, oriented clockwise.
where C is the triangle formed by the lines y = -x + 1, x = 0 and y = 0, oriented clockwise.
(Multiple Choice)
4.8/5  (35)
(35)
Evaluate 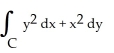 clockwise around the triangle with vertices (0, 0), (3, 0), and (3, 3).
clockwise around the triangle with vertices (0, 0), (3, 0), and (3, 3).
(Multiple Choice)
4.8/5  (36)
(36)
Showing 21 - 40 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)