Exam 17: Vector Calculus
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Let C be a non-self-intersecting closed curve in the xy-plane oriented counterclockwise and bounding a region R having area A and centroid 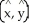 . In terms of these quantities, evaluate the line integral
. In terms of these quantities, evaluate the line integral 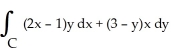 .
.
(Multiple Choice)
4.9/5  (40)
(40)
Find the flux of F = x i + 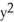 j +
j + 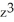 k out of the cube bounded by the coordinate planes and the planes
k out of the cube bounded by the coordinate planes and the planes 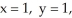 and
and 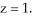
(Multiple Choice)
4.8/5  (31)
(31)
Using spherical polar coordinates, find 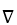 . F for F =
. F for F = 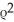 sin( )
sin( )  + sin(
+ sin( 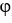 )
) 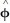 +
+ 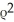 cos( 11ee7bb1_1f6d_7966_ae82_e9760b18acae_TB9661_11 )
cos( 11ee7bb1_1f6d_7966_ae82_e9760b18acae_TB9661_11 )  .
.
(Multiple Choice)
4.7/5  (44)
(44)
Given F = 4y i + x j + 2z k, find 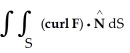 over the hemisphere
over the hemisphere 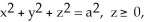 with outward normal
with outward normal  .
.
(Multiple Choice)
4.9/5  (36)
(36)
If r = x i + y j + z k and r = |r|, evaluate and simplify div 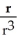 .
.
(Multiple Choice)
4.9/5  (34)
(34)
Evaluate the surface integral 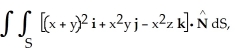 where
where  is the unit inner normal to the surface S of the region lying between the two paraboloids
is the unit inner normal to the surface S of the region lying between the two paraboloids 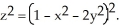
(Multiple Choice)
4.9/5  (37)
(37)
Compute the divergence and the curl of the vector field r = x i + y j + z k.
(Multiple Choice)
4.9/5  (40)
(40)
Calculate the divergence of the vector field F = 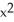 y i +
y i + 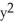 x j + xyz k.
x j + xyz k.
(Multiple Choice)
4.8/5  (29)
(29)
Let w be a function of x, y, and z having continuous second partial derivatives.Calculate curl grad w in terms of those partials.
(Multiple Choice)
4.8/5  (42)
(42)
Find the flux of r = x i + y j + z k out of the cone with base 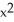 +
+ 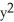 16, z = 0, and vertex at (0, 0, 3).
16, z = 0, and vertex at (0, 0, 3).
(Multiple Choice)
4.8/5  (44)
(44)
Showing 81 - 92 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)