Exam 8: Applications of Integration
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Determine the centroid of the finite plane region bounded by y = x3 and y = 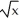 .
.
(Multiple Choice)
4.9/5  (48)
(48)
Find the area of the surface generated by rotating y = 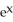 , - x 0 about y = 0.
, - x 0 about y = 0.
(Multiple Choice)
5.0/5  (42)
(42)
What is the present value of a constant, continual stream of payments at a rate of $10,000 per year to continue forever starting 10 years from now? Assume an interest rate of 8% per annum, compounded continuously. Round to the nearest dollar.
(Multiple Choice)
4.9/5  (39)
(39)
A triangle T has vertices ( 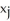 ,
,  ), j = 1, 2, 3 (where each
), j = 1, 2, 3 (where each 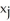 > 0). If the volume of the solid of revolution obtained by revolving T about the y-axis is 2 cubic units, what is the area of T?
> 0). If the volume of the solid of revolution obtained by revolving T about the y-axis is 2 cubic units, what is the area of T?
(Multiple Choice)
4.9/5  (29)
(29)
A pyramid has a triangular base of area A and has a height of h measured perpendicular to the plane of the base. Determine the volume of the pyramid.
(Multiple Choice)
4.9/5  (41)
(41)
Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ![Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ].](https://storage.examlex.com/TB9661/11ee77e1_77f6_6f9b_a0f8_19a5a84c4321_TB9661_11.jpg) ].
].
(Multiple Choice)
4.8/5  (32)
(32)
Find the volume of a solid generated when the region under the curve y = sin x and above the x-axis from x = 0 to x = is rotated about the x-axis.
(Multiple Choice)
4.8/5  (35)
(35)
Find the volume of the solid generated when the region lying under the curve y = 4 - x2 and above the x-axis is rotated about the line y = -1.
(Multiple Choice)
4.9/5  (39)
(39)
The equations y = x3, y = 0, and x = 1 define the bounds of a plane region. Find the volume of the solid obtained by rotating the region about the x-axis.
(Multiple Choice)
4.8/5  (34)
(34)
Find the centroid of the plane quadrilateral region with corners at (0, 0), (0, 2), (2, 3), and (1, 0).
(Multiple Choice)
4.8/5  (37)
(37)
The equations y2 = 4x and x2 = 4y define the bounds of a plane region. Find the volume of the solid obtained by rotating the region to the right of the curve y2 = 4x and above the curve x2 = 4y about
(a) the x-axis and
(b) the y-axis.
(Multiple Choice)
4.9/5  (24)
(24)
A normal distribution has a standard deviation of 25, and about 2.3% values are below 10. Find the mean for this distribution.
(Multiple Choice)
4.9/5  (44)
(44)
What is the present value of a constant, continual stream of payments at a rate of $10,000 per year to continue forever starting now? Assume an interest rate of 8% per annum, compounded continuously.
(Multiple Choice)
4.9/5  (28)
(28)
A triangular plate has vertices at (0, 0), (a, 0), and (0,b), where a > 0 and b > 0. The plate has variable thickness; at position (x, y) its thickness is 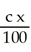 . Assuming the plate is made of material of constant density, find the x-coordinate of its centre of mass.
. Assuming the plate is made of material of constant density, find the x-coordinate of its centre of mass.
(Short Answer)
4.9/5  (43)
(43)
Hooke's law states that the force required to stretch or compress a spring to x units longer or shorter than its natural length is, for sufficiently small values of x, proportional to x. That is, F(x) = kx for some constant k, called the spring constant. Suppose that a force of 10 N is required to stretch a spring by 5 cm. Find the work done in stretching the spring that far.
(Multiple Choice)
5.0/5  (40)
(40)
Find the centroid of the region in the first quadrant bounded by the lines y = 5x, y = x, and x = 4.
(Multiple Choice)
4.9/5  (45)
(45)
The plane region defined by 0 y 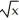 , 0 x a is revolved about the x-axis to generate a 3-dimensional region that is filled with material of constant density. Where is the centre of mass of this material?
, 0 x a is revolved about the x-axis to generate a 3-dimensional region that is filled with material of constant density. Where is the centre of mass of this material?
(Multiple Choice)
4.9/5  (30)
(30)
Find the moment about the x-axis of the region in the first quadrant bounded by the lines y = 5x, y = 3x, x = 3. Assume the areal density is 1.
(Multiple Choice)
4.8/5  (32)
(32)
Showing 21 - 40 of 139
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)