Exam 8: Applications of Integration
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Find the value of the constant real number C so that f(x) = C(x - ![Find the value of the constant real number C so that f(x) = C(x - ) is a probability density function on the interval [0 , 1].](https://storage.examlex.com/TB9661/11ee77e1_77fa_66df_a0f8_3d9971a7929d_TB9661_11.jpg) ) is a probability density function on the interval [0 , 1].
) is a probability density function on the interval [0 , 1].
(Multiple Choice)
4.7/5  (41)
(41)
The plane region defined by 0 ≤ y ≤ 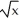 , 0 ≤ x ≤ a is revolved about the x-axis to generate a 3-dimensional region that is filled with material of constant density. Where is the centre of mass of this material?
, 0 ≤ x ≤ a is revolved about the x-axis to generate a 3-dimensional region that is filled with material of constant density. Where is the centre of mass of this material?
(Essay)
4.8/5  (37)
(37)
The random variable T has density function f(t), where f(t) = 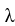
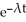 if t 0 and 11ee7b36_e41e_108a_ae82_6b99642b54b5_TB9661_11 is a positive constant. Find the standard deviation of T.
if t 0 and 11ee7b36_e41e_108a_ae82_6b99642b54b5_TB9661_11 is a positive constant. Find the standard deviation of T.
(Multiple Choice)
4.8/5  (44)
(44)
Find the centroid of the region bounded by the x-axis and the curve y = -16 + 10 x - x2.
(Multiple Choice)
4.8/5  (32)
(32)
A supplier of cell phones realizes a marginal revenue of 25 - 15 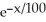 dollars per cell phone when he has sold x cell phones. What will be his total revenue from the sale of 100 cell phones?
dollars per cell phone when he has sold x cell phones. What will be his total revenue from the sale of 100 cell phones?
(Multiple Choice)
4.7/5  (41)
(41)
Find the solution of the initial-value problem 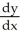 = 3
= 3 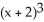 , y(0) = 0.
, y(0) = 0.
(Multiple Choice)
4.8/5  (32)
(32)
A conical reservoir (vertex down) having diameter 10 m and height 10 m is filled with a liquid of density 900 kg/m3. How many kilogram metres of work must be done to pump the liquid out over the top of the tank?
(Multiple Choice)
4.8/5  (32)
(32)
The equations x = -1, x = 0, y = 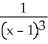 , and y = 0 define the bounds of a region of the plane. Find the volume of the solid obtained by rotating the region about the x-axis.
, and y = 0 define the bounds of a region of the plane. Find the volume of the solid obtained by rotating the region about the x-axis.
(Multiple Choice)
4.8/5  (41)
(41)
For what real values of the constant k does the region lying under the curve y = 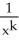 above the x-axis and to the right of the line x = 1 have infinite area but gives rise to a solid with finite volume when rotated about the x-axis?
above the x-axis and to the right of the line x = 1 have infinite area but gives rise to a solid with finite volume when rotated about the x-axis?
(Multiple Choice)
4.8/5  (34)
(34)
Find the volume of the solid obtained by rotating the region inside the circle x2 + y2 = 6 and above the parabola y = x2 about the y-axis.
(Multiple Choice)
4.9/5  (40)
(40)
Find the centre of mass of a system of point masses m1 = 6, m2 = 3, m3 = 2, and m4 = 9 located at (3, -2), (0, 0), (-5, 3), and (4, 2), respectively.
(Multiple Choice)
4.7/5  (37)
(37)
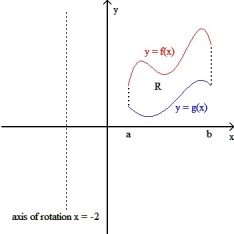
If R is the region enclosed by the graphs of y = f(x) and y = g(x) from x = a to x = b (as shown in the figure below), then the volume V of the solid generated by revolving the region R about the line x = -2 is V = 2 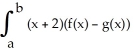 dx.
dx.
(True/False)
4.8/5  (32)
(32)
Find the volume of the solid obtained by rotating about the x-axis the plane region lying under the x-axis and above the curve y = x2 - 2x.
(Multiple Choice)
4.8/5  (42)
(42)
A force of f pounds acting along the x-axis varies according to f(x) = x2 + 3x - 2. Find the work it does on an object that moves from x = -2 to x = 2.
(Multiple Choice)
4.9/5  (40)
(40)
Find a general solution of the first-order linear differential equation 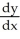 + 3y = e6x.
+ 3y = e6x.
(Multiple Choice)
4.8/5  (36)
(36)
Let X have density function f(x), where f(x) = 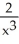 when x 1. Find the mean and standard deviation of X.
when x 1. Find the mean and standard deviation of X.
(Multiple Choice)
4.7/5  (40)
(40)
Find the centroid of the finite plane region bounded by y = x2 and y = x.
(Multiple Choice)
4.8/5  (37)
(37)
Find an integrating factor for the differential equation 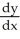 + y = x.
+ y = x.
(Multiple Choice)
4.9/5  (40)
(40)
Find the volume of the solid generated by revolving the triangular region bounded by the lines y = x, y = -x, and x = a (where a > 0) about its edge x = a.
(Multiple Choice)
4.9/5  (34)
(34)
Showing 101 - 120 of 139
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)