Exam 8: Applications of Integration
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
The equations x = 2, x = 4, y = 1/x, and y = 0 define the bounds of a region of the plane. Find the volume of the solid obtained by rotating the region about the x-axis.
(Multiple Choice)
4.9/5  (34)
(34)
Given that the area of a sphere of radius r is 4 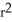
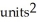 , find the centroid of the semicircular arc.
, find the centroid of the semicircular arc. 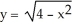 .
.
(Multiple Choice)
4.8/5  (46)
(46)
A tank is in the shape of a right circular cone with top radius 2 m and height 5 m. It contains water up to the height of 4 m. The density of water is 1,000 kg/m3. How much work must be done to pump all of the water out of the tank over the top edge of the tank?
(Multiple Choice)
4.8/5  (43)
(43)
A conical tank with vertex at the bottom and top radius 10 cm is 40 cm tall. It is filled with a substance whose density at depth y cm is (2 + y) g/ 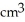 . Find the total mass of the substance filling the tank.
. Find the total mass of the substance filling the tank.
(Multiple Choice)
4.9/5  (38)
(38)
Find the centroid of the planar region bounded by y =  , y = 0, x = 1, and x = 2.
, y = 0, x = 1, and x = 2.
(Multiple Choice)
4.8/5  (42)
(42)
Find a general solution to the first-order linear differential equation 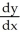 - 2y -
- 2y - 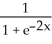 = 0.
= 0.
(Multiple Choice)
4.9/5  (28)
(28)
Find the centroid of the finite plane region bounded by y = 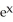 , y =
, y = 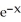 , and x = 1.
, and x = 1.
(Multiple Choice)
4.8/5  (33)
(33)
Determine the solution of the differential equation 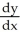 = (1 - 2x)
= (1 - 2x) 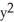 that satisfies the condition y(0) = -
that satisfies the condition y(0) = - 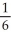 .
.
(Multiple Choice)
4.8/5  (37)
(37)
An experiment has six possible outcomes with values X from 0 to 5 inclusive. The probability of the outcome with value j is proportional to 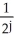 . Find the mean and standard deviation of the distribution of values X.
. Find the mean and standard deviation of the distribution of values X.
(Multiple Choice)
4.8/5  (43)
(43)
A motorboat is travelling with a velocity of 40 ft/sec when its motor shuts off at time t = 0. Thereafter its deceleration, due to water resistance, is given by 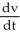 = -k
= -k 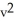 where k is a positive constant. After 10 seconds, the boat's velocity is measured to be 20 ft/sec.
(a) What is the value of k?
(b) When will the boat slow to 5 ft/sec?
where k is a positive constant. After 10 seconds, the boat's velocity is measured to be 20 ft/sec.
(a) What is the value of k?
(b) When will the boat slow to 5 ft/sec?
(Multiple Choice)
4.8/5  (40)
(40)
Find the general solution of the differential equation 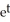
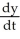 + t
+ t 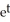 y =
y = 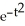 (t + 1).
(t + 1).
(Multiple Choice)
4.8/5  (39)
(39)
A tank contains 200 litres of fluid in which 60 grams of salt is dissolved. A brine solution of 2 grams of salt per litre is pumped into the tank at a rate of 2 litres/minute. The well-stirred solution is then pumped out at the same rate.(a) Write the differential equation in terms of Q(t) and t and write the initial condition to model this problem. (Q(t) should represent the amount of salt in the tank at time t).(b) Solve the equation in part (a).(c) How much salt will be present in the tank after a long period of time?
(Multiple Choice)
4.7/5  (29)
(29)
Find a general solution to the first-order linear differential equation x 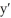 + y = x3.
+ y = x3.
(Multiple Choice)
4.8/5  (38)
(38)
Find the moment about the x-axis of a thin plate that occupies the planar region described by 0 y 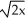 , 0 x 1 if the areal density is given by
, 0 x 1 if the areal density is given by 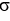 (x) = ex.
(x) = ex.
(Multiple Choice)
4.8/5  (27)
(27)
Find the coordinates of the centroid of the region enclosed by y = sin(x) and the x-axis from x = 0 to 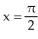 .
.
(Multiple Choice)
4.8/5  (30)
(30)
Find the volume of a right circular cone of base radius r and height h.
(Multiple Choice)
4.8/5  (33)
(33)
A cylindrical tank 8 m in diameter and 8 m high, with axis vertical, has 6 m of water in it. How many kilogram metres of work must be done to pump half the water in the tank to a height of 8 m above the top of the tank? (1 m3 of water weighs 1,000 kg.)
(Multiple Choice)
4.8/5  (33)
(33)
Showing 41 - 60 of 139
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)