Exam 8: Applications of Integration
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
A random variable X is normally distributed with mean 100 and standard deviation 20. Below what value of X does 25% of the probability lie?
(Multiple Choice)
4.8/5  (39)
(39)
For what constant k if f(x) = k ![For what constant k if f(x) = k a probability density function on [0, 1]?](https://storage.examlex.com/TB9661/11ee77e1_77fa_3fc8_a0f8_fd9eea863aff_TB9661_11.jpg) a probability density function on [0, 1]?
a probability density function on [0, 1]?
(Multiple Choice)
4.8/5  (34)
(34)
Interior to the Earth, the gravitational attraction varies directly as the distance from the centre of the Earth. What is the work necessary to lift a mass weighing 1 kg at the surface from the centre to the surface? Assume that the radius of the Earth is 6,400 km and the force of attraction of the Earth on a 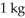 mass at its surface is 9.8 Newtons.
mass at its surface is 9.8 Newtons.
(Multiple Choice)
4.8/5  (39)
(39)
Find, correct to 4 decimal places, the length of the curve y = 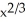 from x = 1 to x = 8.
from x = 1 to x = 8.
(Multiple Choice)
4.7/5  (42)
(42)
Find the volumes of solids generated when the ellipse 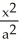 +
+ 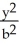 = 1 (where a > 0 and b > 0) is rotated about (a) the x-axis and (b) the y-axis.
= 1 (where a > 0 and b > 0) is rotated about (a) the x-axis and (b) the y-axis.
(Multiple Choice)
4.9/5  (42)
(42)
The base of a certain solid is a circular disk of radius a cm. Cross-sections of the solid in planes perpendicular to a specific diameter of the base are equilateral triangles. Find the volume of the solid.
(Multiple Choice)
4.9/5  (32)
(32)
Find the solution of the initial value problem 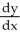 =
= 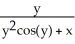 , y(π/2) = -
, y(π/2) = - 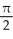 .
.
(Short Answer)
4.8/5  (33)
(33)
Find the area of the surface obtained by rotating the curve y = 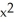 , -1 x 1, about the x-axis.
, -1 x 1, about the x-axis.
(Multiple Choice)
4.9/5  (29)
(29)
Suppose the thickness of the blacktop on a road that has recently been resurfaced is normal with a mean of 6 cm and a standard deviation of 0.4 cm. What percentage of the blacktop is at least 5 cm thick?
(Multiple Choice)
4.8/5  (32)
(32)
Find the family of curves each of which intersects all of the hyperbolas x2 - y2 = C at right angles.
(Essay)
4.9/5  (40)
(40)
A triangular plate has vertices at (0, 0), (a, 0), and (0, b), where a > 0 and b > 0. The plate has variable thickness; at position (x, y) its thickness is 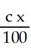 . Assuming the plate is made of material of constant density, find the x-coordinate of its centre of mass.
. Assuming the plate is made of material of constant density, find the x-coordinate of its centre of mass.
(Multiple Choice)
4.9/5  (45)
(45)
Plutonium 239 decays continuously at a rate of 0.00284% per year. If X is the time a randomly chosen plutonium atom will decay, write down the associated probability density function and use it to compute the probability that a plutonium atom will decay between 100 and 500 years from now.
(Essay)
4.8/5  (47)
(47)
A certain solid S has a horizontal plane region R as its base and has height h cm measured perpendicular to R. For 0 < z < h, the volume of that part of S lying beneath the plane at height z cm above R is V(z) = 2z + z3 cm3. Find (a) the area of the cross-section of S in the plane at height z cm and (b) the area of R.
(Multiple Choice)
4.8/5  (38)
(38)
Find the length of the closed loop part of the curve 3 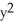 = x
= x 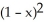 .
.
(Multiple Choice)
4.8/5  (41)
(41)
A vertical cylindrical container 10 m high and 6 m in diameter is half full of water. Find, to 4 significant figures, the amount of work done in pumping all the water out at the top of the container given that the density of water is 1,000 kg/m3.
(Multiple Choice)
4.9/5  (39)
(39)
If R is the region enclosed by the graphs of y = f(x) and y = g(x) from x = a to x = b (as shown in the figure below), then the volume V of the solid generated by revolving the region R about the line y = -2 is V = 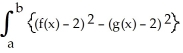 dx.
dx.
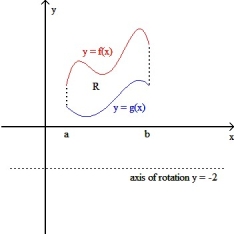
(True/False)
4.9/5  (39)
(39)
Use Pappus's Theorem to find the volume of the solid generated by revolving the region R enclosed by y = 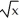 , x = 0, and y =1 about the line y = -1 given that the centroid of the region R is at the point(
, x = 0, and y =1 about the line y = -1 given that the centroid of the region R is at the point(  ,
,  ) = (
) = ( 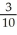 ,
,  ).
).
(Essay)
4.7/5  (31)
(31)
The region R is bounded by y = ln x, y = 0, x = 1, and x = 2. Find the volume of the solid obtained by revolving R about the y-axis.
(Multiple Choice)
4.7/5  (28)
(28)
Showing 121 - 139 of 139
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)