Exam 8: Applications of Integration
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Use Pappus's Theorem to find the volume of the solid of revolution obtained by rotating the triangular plane region specified by 0 y 1 -  about (a) the line x = 2 and(b) the line y = 2.
about (a) the line x = 2 and(b) the line y = 2.
(Multiple Choice)
4.9/5  (29)
(29)
Find the centre of mass of the semicircular plate 0 y 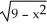 assuming it has constant density.
assuming it has constant density.
(Multiple Choice)
4.9/5  (34)
(34)
Find the volume of a solid formed by revolving the disk bounded by a circle of radius a cm about a line tangent to that circle.
(Multiple Choice)
4.7/5  (41)
(41)
Find the length of the arc y = ln(sec x) between x = 0 and x = 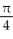 .
.
(Multiple Choice)
4.9/5  (38)
(38)
Find the solution of the initial-value problem 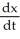 =
= 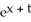 , x(0) = a.
, x(0) = a.
(Multiple Choice)
4.9/5  (36)
(36)
Assuming the Earth is spherical with radius 6378 km, find the area of the surface of the Earth between the Tropic of Cancer (23.5° north latitude) and the Antarctic Circle (66.5° south latitude) as shown in the figure below.
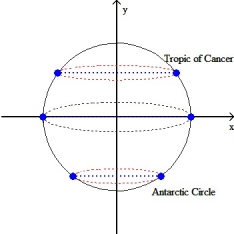
(Short Answer)
4.9/5  (35)
(35)
Let A(x) be the cross-sectional area of a solid by planes perpendicular to the x-axis. If the volume of the solid that lies between x = 1 and x = z > 1 is V = 4 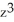 + 2, find A(x).
+ 2, find A(x).
(Multiple Choice)
4.8/5  (38)
(38)
The region R is the portion of the first quadrant that is below the parabola y2 = 8x and above the hyperbola y2 - x2 = 15. Find the volume of the solid obtained by revolving R about the x-axis.
(Multiple Choice)
4.7/5  (39)
(39)
The plane region bounded by the curve 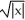 +
+ 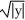 = 1 is revolved about the line x = 2. Find the volume of the solid generated.
= 1 is revolved about the line x = 2. Find the volume of the solid generated.
(Multiple Choice)
4.8/5  (47)
(47)
Consider the finite plane region bounded by the coordinate axes and the line 4x + 3y = 12. Assuming the region has constant areal density 1, find the moments of this region about the coordinate axes.
(Multiple Choice)
5.0/5  (42)
(42)
Find the volume of a solid whose base is the region in the first quadrant bounded by the line  and the coordinate axes if every planar section perpendicular to the x-axis is a semicircle.
and the coordinate axes if every planar section perpendicular to the x-axis is a semicircle.
(Multiple Choice)
4.8/5  (44)
(44)
Determine the solution of the differential equation that satisfies the boundary conditions 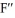 (x) = 8,
(x) = 8, 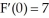 ,
, 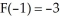 .
.
(Multiple Choice)
4.9/5  (32)
(32)
Let R be the plane region enclosed by the graphs of y = f(x) and y = g(x) from x = a to x = b , where a > 0(as shown in the figure below).If the solid generated by revolving the plane region R about the x-axis has the same volume as the solid generated by revolving the region R about the y-axis , then f and g satisfy which equation for all x > 0?
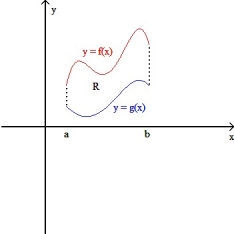
(Multiple Choice)
4.9/5  (33)
(33)
Find the mass of a thin plate that occupies the planar region described by 0 y sin(2x), 0 x 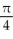 if the areal density is given by
if the areal density is given by 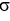 (x) = 8x.
(x) = 8x.
(Multiple Choice)
4.9/5  (39)
(39)
Find the volume of an elliptical cone whose base in the horizontal xy-plane is the elliptic disk 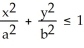 (where a > 0 and b > 0) and whose vertex is at height h directly above the centre of the base.
(where a > 0 and b > 0) and whose vertex is at height h directly above the centre of the base.
(Multiple Choice)
4.8/5  (41)
(41)
The force of gravity (outside the Earth) attracting a mass m is proportional to the mass m and inversely proportional to the square of the distance from the centre of the Earth. Find the work done in moving a mass that weighs 1 lb at the surface of the Earth to 10 miles above the surface. Assume the radius of the Earth is 4,000 mi. At the Earth's surface, a force of 1 lb is required to lift a mass of 1 lb.
(Multiple Choice)
4.9/5  (35)
(35)
A notch is cut out of a vertical cylindrical log of radius r cm by two planar saw cuts that meet along a horizontal line passing through the centre of the log. If the saw cuts make angles ± 30º with the horizontal (so that the angle of the notch is 60º), find the volume of wood cut out of the log in making the notch.
(Multiple Choice)
4.8/5  (45)
(45)
Showing 61 - 80 of 139
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)