Exam 18: Model Building
Exam 1: What Is Statistics46 Questions
Exam 2: Graphical Descriptive Techniques 194 Questions
Exam 3: Graphical Descriptive Techniques 2156 Questions
Exam 4: Numerical Descriptive Techniques275 Questions
Exam 5: Data Collection and Sampling84 Questions
Exam 6: Probability240 Questions
Exam 7: Random Variables and Discrete Probability Distributions283 Questions
Exam 8: Continuous Probability Distributions224 Questions
Exam 9: Sampling Distributions156 Questions
Exam 10: Introduction to Estimation154 Questions
Exam 11: Introduction to Hypothesis Testing189 Questions
Exam 12: Inference About a Population153 Questions
Exam 13: Inference About Comparing Two Populations170 Questions
Exam 14: Analysis of Variance157 Questions
Exam 15: Chi-Squared Tests179 Questions
Exam 16: Simple Linear Regression and Correlation304 Questions
Exam 17: Multiple Regression160 Questions
Exam 18: Model Building148 Questions
Exam 19: Nonparametric Statistics175 Questions
Exam 20: Time-Series Analytics and Forecasting225 Questions
Exam 21: Statistical Process Control140 Questions
Exam 22: Decision Analysis123 Questions
Exam 23: Conclusion47 Questions
Select questions type
To gather the required observations for your potential regression models,a general rule is that there should be at least ____________________ observations for each independent variable used in the equation.
(Short Answer)
4.9/5  (32)
(32)
In explaining the amount of money spent on gifts for a child's birthday each year,the independent variable,age of child,is best represented by a dummy variable.
(True/False)
4.8/5  (37)
(37)
The model 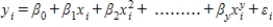 is referred to as a polynomial model with one predictor variable.
is referred to as a polynomial model with one predictor variable.
(True/False)
4.8/5  (36)
(36)
Computer Training
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s).  Use statistical software to answer the following question(s).
-{Computer Training Narrative} Develop an estimated regression equation of the form
Use statistical software to answer the following question(s).
-{Computer Training Narrative} Develop an estimated regression equation of the form 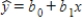 .
.
(Essay)
4.8/5  (36)
(36)
In regression analysis,a nominal independent variable such as color,with three different categories such as red,white,and blue,is best represented by three indicator variables to represent the three colors.
(True/False)
4.9/5  (35)
(35)
Hockey Teams
An avid hockey fan was in the process of examining the factors that determine the success or failure of hockey teams.He noticed that teams with many rookies and teams with many veterans seem to do quite poorly.To further analyze his beliefs he took a random sample of 20 teams and proposed a second-order model with one independent variable,average years of professional experience.The selected model is y = β0 + β1x + β2x2 + ε,where y = winning team's percentage,and x = average years of professional experience.The computer output is shown below. THE REGRESSION EQUATION IS y = 32.6 + 5.96x− .48x2  S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE
S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE 
-{Hockey Teams Narrative} What is the coefficient of determination? Explain what this statistic tells you about the model.
-{Hockey Teams Narrative} What is the coefficient of determination? Explain what this statistic tells you about the model.
(Essay)
4.9/5  (40)
(40)
For the following regression equation 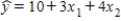 ,a unit increase in x2 increases the value of y on average by:
,a unit increase in x2 increases the value of y on average by:
(Multiple Choice)
4.8/5  (35)
(35)
Suppose that the sample regression equation of a model is 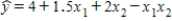 .If we examine the relationship between x1 and y for four different values of x2,we observe that the four equations produced differ only in the intercept term.
.If we examine the relationship between x1 and y for four different values of x2,we observe that the four equations produced differ only in the intercept term.
(True/False)
4.8/5  (29)
(29)
In order to represent 3 categories of a nominal variable,we need to create _______________ indicator variables.
(Short Answer)
4.8/5  (37)
(37)
Discuss briefly the procedure that is employed in the building of a model.
(Essay)
4.9/5  (31)
(31)
In a first-order polynomial model with no interaction,the effect of x1 on y remains the same no matter what the value of x2 is.The graph of this model produces straight lines that are ____________________ to each other.
(Short Answer)
4.8/5  (36)
(36)
Incomes of Physicians
An economist is analyzing the incomes of physicians (general practitioners,surgeons,and psychiatrists).He realizes that an important factor is the number of years of experience.However,he wants to know if there are differences among the three professional groups.He takes a random sample of 125 physicians and estimates the multiple regression model y = β0 + β1x1 + β2x2 + β3x3 + ε,where y = annual income (in $1,000),x1 = years of experience,x2 = 1 if physician and 0 if not,and x3 = 1 if surgeons and 0 if not.The computer output is shown below. THE REGRESSION EQUATION IS y = 71.65 + 2.07x1 + 10.16x2− 7.44x3  S = 42.6 R−Sq = 30.9% ANALYSIS OF VARIANCE
S = 42.6 R−Sq = 30.9% ANALYSIS OF VARIANCE 
-{Incomes of Physicians Narrative} Is there enough evidence at the 5% significance level to conclude that income and experience are linearly related?
-{Incomes of Physicians Narrative} Is there enough evidence at the 5% significance level to conclude that income and experience are linearly related?
(Essay)
4.8/5  (42)
(42)
Silver Prices
An economist is in the process of developing a model to predict the price of silver.She believes that the two most important variables are the price of a barrel of oil (x1)and the interest rate (x2).She proposes the first-order model with interaction: y = β0 + β1x1 + β2x2 + β3x1x3 + ε.A random sample of 20 daily observations was taken.The computer output is shown below. THE REGRESSION EQUATION IS y = 115.6 + 22.3x1 + 14.7x2− 1.36x1x2  S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE
S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE 
-{Silver Prices Narrative} Do these results allow us at the 5% significance level to conclude that the model is useful in predicting the price of silver?
-{Silver Prices Narrative} Do these results allow us at the 5% significance level to conclude that the model is useful in predicting the price of silver?
(Essay)
4.8/5  (34)
(34)
Motorcycle Fatalities
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model 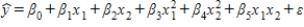 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 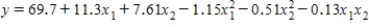
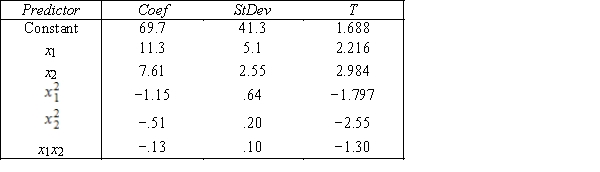 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
-{Motorcycle Fatalities Narrative} Test at the 1% significance level to determine if the x2 term should be retained in the model.
-{Motorcycle Fatalities Narrative} Test at the 1% significance level to determine if the x2 term should be retained in the model.
(Essay)
4.8/5  (39)
(39)
Hockey Teams
An avid hockey fan was in the process of examining the factors that determine the success or failure of hockey teams.He noticed that teams with many rookies and teams with many veterans seem to do quite poorly.To further analyze his beliefs he took a random sample of 20 teams and proposed a second-order model with one independent variable,average years of professional experience.The selected model is y = β0 + β1x + β2x2 + ε,where y = winning team's percentage,and x = average years of professional experience.The computer output is shown below. THE REGRESSION EQUATION IS y = 32.6 + 5.96x− .48x2  S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE
S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE 
-{Hockey Teams Narrative} Test to determine at the 10% significance level if the linear term should be retained.
-{Hockey Teams Narrative} Test to determine at the 10% significance level if the linear term should be retained.
(Essay)
4.9/5  (33)
(33)
The stepwise regression procedure begins by computing the simple regression model for each independent variable.
(True/False)
4.7/5  (38)
(38)
Indicator variables can assume as many values as there are categories of its corresponding nominal variable.
(True/False)
4.9/5  (38)
(38)
When the dependent variable is nominal,a(n)____________________ regression model is used.
(Short Answer)
4.9/5  (36)
(36)
Showing 41 - 60 of 148
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)