Question 1

A certain molecule has 2.00 eV of rotational energy in the l = 1 state. In the l = 4 state, what would its rotational energy be?

Accepted Answer

A)  8.00 eV 
B)  16.0 eV 
C)  20.0 eV 
D)  30.0 eV 
E)  32.0 eV 
A)  8.00 eV 
B)  16.0 eV 
C)  20.0 eV 
D)  30.0 eV 
E)  32.0 eV

Question 2

The spacing of the atoms (treated as point masses) in the H2 molecule is 7.4 x 10-11 m. What is the energy of the l = 1 rotational level? (1 eV = 1.60 × 10-19 J, h = 6.626 × 10-34 J ∙ s,   = 1.055 × 10-34 J ∙ s, mH ≈ mproton = 1.67 × 10-27 kg)

Accepted Answer

A)  0.090 eV 
B)  0.070 eV 
C)  0.045 eV 
D)  0.030 eV 
E)  0.015 eV 
A)  0.090 eV 
B)  0.070 eV 
C)  0.045 eV 
D)  0.030 eV 
E)  0.015 eV

Question 3

If a metal had a Fermi level (energy) of 5.0 eV, what would be the average energy of the electrons at 0 K?

Accepted Answer

A)  8.0 eV 
B)  6.0 eV 
C)  3.0 eV 
D)  0.00 eV 
E)  5.0 eV 
A)  8.0 eV 
B)  6.0 eV 
C)  3.0 eV 
D)  0.00 eV 
E)  5.0 eV

Question 4

A diatomic molecule has 2.6 × 10-5 eV of rotational energy in the l = 2 quantum state. What is its rotational energy in the l = 1 quantum state?

Accepted Answer

A)  3.4 µeV 
B)  4.1 µeV 
C)  5.3 µeV 
D)  7.8 µeV 
E)  8.7 µeV 
A)  3.4 µeV 
B)  4.1 µeV 
C)  5.3 µeV 
D)  7.8 µeV 
E)  8.7 µeV

Question 5

In a p-type semiconductor, a hole is

Accepted Answer

A)  a donor atom. 
B)  an extra electron supplied by a donor atom. 
C)  an extra proton supplied by a donor atom. 
D)  a missing atom in the crystalline structure. 
E)  a region where an electron is missing. 
A)  a donor atom. 
B)  an extra electron supplied by a donor atom. 
C)  an extra proton supplied by a donor atom. 
D)  a missing atom in the crystalline structure. 
E)  a region where an electron is missing.

Question 6

For a solid in which the occupation of the energy states is given by the Fermi-Dirac distribution, the probability that a certain state is occupied at a temperature T0 is 0.70. If the temperature is doubled to 2T0, what is the probability that the same state is occupied? Assume that the Fermi energy does not change with temperature.

Accepted Answer

The answer of For a solid in which the occupation...

Question 7

A diatomic molecule is vibrating in its first excited quantum state above the ground state. In that excited state, its frequency is 2.0 × 1013 Hz. What is the energy of the molecule in this state? (h = 6.626 × 10-34 J ∙ s,   = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J

Accepted Answer

A)  0.041 eV 
B)  0.083 eV 
C)  0.12 eV 
D)  0.15 eV 
E)  0.17 eV 
A)  0.041 eV 
B)  0.083 eV 
C)  0.12 eV 
D)  0.15 eV 
E)  0.17 eV

Question 8

19) Silver has a Fermi level (energy) of 5.5 eV. At 0 K, at what speed would the electrons be moving if they had kinetic energy equal to the Fermi energy? (This speed is known as the Fermi speed.) (mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J, h = 6.626 × 10-34 J ∙ s)

Accepted Answer

A)  1400 km/s 
B)  1.0 km/s 
C)  2.2 km/s 
D)  1100 km/s 
E)  3.5 km/s 
A)  1400 km/s 
B)  1.0 km/s 
C)  2.2 km/s 
D)  1100 km/s 
E)  3.5 km/s

Question 9

The Fermi energy of rubidium at a temperature of 5 K is 1.85 eV. An electron state in rubidium is 0.007 eV above the Fermi level. What is the probability that this state is occupied at a temperature of 9K? (mel = 9.11 × 10-31 kg, h = 6.626 × 10-34 J ∙ s, Boltzmann constant = 1.38 ∙ 10-23 J/K, 1 eV = 1.60 × 10-19 J)

Accepted Answer

A)  1 × 10-4 
B)  2 × 10-5 
C)  5 × 10-6 
D)  1 × 10-6 
E)  2 × 10-7 
A)  1 × 10-4 
B)  2 × 10-5 
C)  5 × 10-6 
D)  1 × 10-6 
E)  2 × 10-7

Question 10

If one metal has double the number of conduction electrons per unit volume of a second metal, then its Fermi level (energy) is how many times that of the second metal?

Accepted Answer

A)  1.41 
B)  2.83 
C)  2.00 
D)  3.22 
E)  1.59 
A)  1.41 
B)  2.83 
C)  2.00 
D)  3.22 
E)  1.59

Question 11

Ionic bonding is due to

Accepted Answer

A)  the sharing of electrons between atoms. 
B)  the transfer of electrons between atoms. 
C)  atoms bonding to hydrogen molecules. 
D)  atoms bonding to oxygen molecules. 
A)  the sharing of electrons between atoms. 
B)  the transfer of electrons between atoms. 
C)  atoms bonding to hydrogen molecules. 
D)  atoms bonding to oxygen molecules.

Exam 41: Molecules and Condensed Matter

A certain molecule has 2.00 eV of rotational energy in the l = 1 state. In the l = 4 state, what would its rotational energy be?

The spacing of the atoms (treated as point masses) in the H2 molecule is 7.4 x 10-11 m. What is the energy of the l = 1 rotational level? (1 eV = 1.60 × 10-19 J, h = 6.626 × 10-34 J ∙ s, = 1.055 × 10-34 J ∙ s, mH ≈ mproton = 1.67 × 10-27 kg)

If a metal had a Fermi level (energy) of 5.0 eV, what would be the average energy of the electrons at 0 K?

A diatomic molecule has 2.6 × 10-5 eV of rotational energy in the l = 2 quantum state. What is its rotational energy in the l = 1 quantum state?

In a p-type semiconductor, a hole is

A diatomic molecule is vibrating in its first excited quantum state above the ground state. In that excited state, its frequency is 2.0 × 1013 Hz. What is the energy of the molecule in this state? (h = 6.626 × 10-34 J ∙ s, = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J

19) Silver has a Fermi level (energy) of 5.5 eV. At 0 K, at what speed would the electrons be moving if they had kinetic energy equal to the Fermi energy? (This speed is known as the Fermi speed.) (mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J, h = 6.626 × 10-34 J ∙ s)

If one metal has double the number of conduction electrons per unit volume of a second metal, then its Fermi level (energy) is how many times that of the second metal?

Ionic bonding is due to

Units, Physical Quantities, and Vectors

Motion Along a Straight Line

Motion in Two or Three Dimensions

Newtons Laws of Motion

Applying Newtons Laws

Work and Kinetic Energy

Potential Energy and Energy Conservation

Momentum, Impulse, and Collisions

Rotation of Rigid Bodies

Equilibrium and Elasticity

Fluid Mechanics

Gravitation

Periodic Motion

Mechanical Waves

Sound and Hearing

Temperature and Heat

Thermal Properties of Matter

The First Law of Thermodynamics

The Second Law of Thermodynamics

Electric Charge and Electric Field

Gausss Law

Electric Potential

Capacitance and Dielectrics

Current, Resistance, and Electromotive Force

Direct-Current Circuits

Magnetic Field and Magnetic Forces

Sources of Magnetic Field

Electromagnetic Induction

Inductance

Alternating Current

Electromagnetic Waves

The Nature and Propagation of Light

Geometric Optics

Interference

Diffraction

Relativity

Photons: Light Waves Behaving As Particles

Particles Behaving As Waves

Quantum Mechanics

Atomic Structure

Nuclear Physics

Particle Physics and Cosmology

Filters

The spacing of the atoms (treated as point masses) in the H₂ molecule is 7.4 x 10^-11 m. What is the energy of the l = 1 rotational level? (1 eV = 1.60 × 10^-19 J, h = 6.626 × 10^-34 J ∙ s, 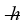= 1.055 × 10^-34 J ∙ s, ^mH ≈ ^mproton = 1.67 × 10^-27kg)

A diatomic molecule has 2.6 × 10^-5 eV of rotational energy in the l = 2 quantum state. What is its rotational energy in the l = 1 quantum state?

A diatomic molecule is vibrating in its first excited quantum state above the ground state. In that excited state, its frequency is 2.0 × 10¹³ Hz. What is the energy of the molecule in this state? (h = 6.626 × 10^-34 J ∙ s, 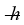= 1.055 × 10^-34 J ∙ s, 1 eV = 1.60 × 10^-19 J

19) Silver has a Fermi level (energy) of 5.5 eV. At 0 K, at what speed would the electrons be moving if they had kinetic energy equal to the Fermi energy? (This speed is known as the Fermi speed.) (^mel = 9.11 × 10^-31 kg, 1 eV = 1.60 × 10^-19 J, h = 6.626 × 10^-34 J ∙ s)