Exam 16: Vector Calculus
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Use Stokes' Theorem to evaluate . ;
C is the boundary of the triangle with vertices , , and oriented in a counterclockwise direction when viewed from above
(Short Answer)
4.8/5  (41)
(41)
Consider the vector field If a particle starts at the point in the velocity field given by F, find an equation of the path it follows.
(Short Answer)
4.8/5  (36)
(36)
Find the exact mass of a thin wire in the shape of the helix if the density is 5.
(Multiple Choice)
4.8/5  (30)
(30)
Evaluate for the vector field F and the path C. (Hint: Show that F is conservative, and pick a simpler path.) C:
(Multiple Choice)
4.8/5  (34)
(34)
Evaluate the surface integral. S is the part of the plane that lies in the first octant.
(Multiple Choice)
4.8/5  (32)
(32)
Determine whether F is conservative. If so, find a function f such that .
(Short Answer)
4.7/5  (36)
(36)
Determine whether or not F is a conservative vector field. If it is, find a function f such that
(Short Answer)
4.9/5  (45)
(45)
A thin wire in the shape of a quarter-circle , , has a linear mass density . Find the mass and the location of the center of mass of the wire.
(Short Answer)
4.9/5  (44)
(44)
Evaluate . ; S is the part of the cone between the planes and .
(Multiple Choice)
4.8/5  (39)
(39)
Find the work done by the force field in moving an object along an arch of the cycloid
(Short Answer)
4.8/5  (36)
(36)
Use Green's Theorem and/or a computer algebra system to evaluate where C is the circle with counterclockwise orientation.
(Multiple Choice)
4.8/5  (35)
(35)
A particle starts at the point , moves along the x-axis to (3, 0) and then along the semicircle to the starting point. Use Green's Theorem to find the work done on this particle by the force field
(Multiple Choice)
4.9/5  (39)
(39)
Find a function f such that and use it to evaluate along the given curve C. C is the upper semicircle that starts at (1, 2) and ends at (5, 2).
(Short Answer)
4.7/5  (39)
(39)
Find the correct identity, if f is a scalar field, F and G are vector fields.
(Multiple Choice)
4.8/5  (35)
(35)
Let where . Which of the following equations does the line segment from to satisy?
(Multiple Choice)
4.8/5  (38)
(38)
Below is given the plot of a vector field F in the xy-plane. (The z-component of F is 0.) By studying the plot, determine whether div F is positive, negative, or zero. 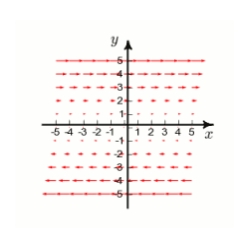
(Multiple Choice)
4.9/5  (39)
(39)
Let F be a vector field. Determine whether the expression is meaningful. If so, state whether the expression represents a scalar field or a vector field.
(Short Answer)
4.8/5  (37)
(37)
Showing 21 - 40 of 137
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)