Exam 16: Vector Calculus
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Use Stokes' Theorem to evaluate . ; C is the curve obtained by intersecting the cylinder with the hyperbolic paraboloid , oriented in a counterclockwise direction when viewed from above
(Multiple Choice)
4.9/5  (34)
(34)
Determine whether F is conservative. If so, find a function f such that .
(Multiple Choice)
4.9/5  (36)
(36)
Let R be a plane region of area A bounded by a piecewise-smooth simple closed curve C. Using Green's Theorem, it can be shown that the centroid of R is , where Use these results to find the centroid of the given region.
The triangle with vertices , , and .
(Short Answer)
4.9/5  (26)
(26)
Use a computer algebra system to compute the flux of F across S. S is the surface of the cube cut from the first octant by the planes
(Multiple Choice)
4.9/5  (43)
(43)
Find the gradient vector field of the scalar function F. (That is, find the conservative vector field F for the potential function f of F.)
(Multiple Choice)
4.9/5  (37)
(37)
A fluid with density flows with velocity Find the rate of flow upward through the paraboloid
(Short Answer)
4.8/5  (25)
(25)
Calculate the work done by the force field when a particle moves under its influence around the edge of the part of the sphere that lies in the first octant, in a counterclockwise direction as viewed from above.
(Short Answer)
4.9/5  (36)
(36)
Find the area of the part of paraboloid that lies inside the cylinder
(Short Answer)
4.7/5  (47)
(47)
Find the area of the surface. The part of the paraboloid ; ,
(Multiple Choice)
4.8/5  (33)
(33)
The flow lines (or streamlines) of a vector field are the paths followed by a particle whose velocity field is the given vector field. Thus, the vectors in a vector field are tangent to the flow lines. The flow lines of the vector field satisfy the differential equations and Solve these differential equations to find the equations of the family of flow lines.
(Short Answer)
4.7/5  (40)
(40)
Find the value of the constant c such that the vector field is the curl of some vector field F.
(Multiple Choice)
4.9/5  (26)
(26)
The plot of a vector field is shown below. A particle is moved . By inspection, determine whether the work done by F on the particle is positive, negative, or zero. 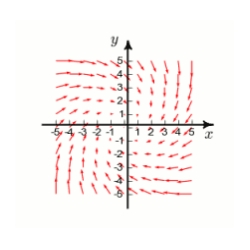
(Short Answer)
4.8/5  (39)
(39)
Find an equation of the tangent plane to the parametric surface represented by r at the specified point. ;
(Short Answer)
4.9/5  (38)
(38)
Use Gauss's Law to find the charge contained in the solid hemisphere , if the electric field is
(Short Answer)
4.8/5  (32)
(32)
Show that F is conservative and find a function f such that , and use this result to evaluate , where C is any path from to . ; and
(Multiple Choice)
4.9/5  (35)
(35)
Evaluate the surface integral. S is the part of the cylinder between the planes and in the first octant.
(Short Answer)
4.8/5  (42)
(42)
Use Green's Theorem to evaluate the line integral along the positively oriented closed curve C. , where C is the cardioid .
(Multiple Choice)
4.9/5  (28)
(28)
Find the work done by the force field F on a particle that moves along the curve C. ; ,
(Multiple Choice)
4.8/5  (40)
(40)
A particle is moving in a velocity field At time t = 1 the particle is located at the point (1, 5, 5).
a). What is the velocity of the particle at t = 1?
b). What is the approximate location of the particle at t = 1.01?
(Short Answer)
4.8/5  (34)
(34)
Showing 41 - 60 of 137
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)