Exam 16: Vector Calculus
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Find a parametric representation for the part of the elliptic paraboloid that lies in front of the plane x = 0.
(Multiple Choice)
4.8/5  (38)
(38)
Let F be a vector field. Determine whether the expression is meaningful. If so, state whether the expression represents a scalar field or a vector field.
curl (div F)
(Short Answer)
4.8/5  (45)
(45)
A thin wire is bent into the shape of a semicircle If the linear density is , find the exact mass of the wire.
(Multiple Choice)
4.8/5  (42)
(42)
Find the area of the surface S where S is the part of the surface that lies inside the cylinder
(Short Answer)
4.9/5  (32)
(32)
Find an equation in rectangular coordinates, and then identify the surface.
(Short Answer)
4.9/5  (32)
(32)
Find a function f such that , and use it to evaluate along the given curve C.
(Short Answer)
4.9/5  (34)
(34)
The plot of a vector field is shown below. A particle is moved . By inspection, determine whether the work done by F on the particle is positive, negative, or zero. 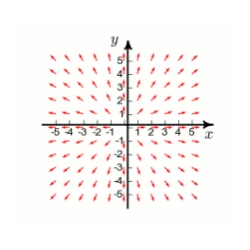
(Short Answer)
5.0/5  (40)
(40)
Evaluate the surface integral. Round your answer to four decimal places. S is surface
(Multiple Choice)
5.0/5  (42)
(42)
Find the work done by the force field on a particle that moves along the parabola
(Multiple Choice)
4.8/5  (34)
(34)
Determine whether or not vector field is conservative. If it is conservative, find a function f such that
(Short Answer)
4.8/5  (34)
(34)
Evaluate the surface integral for the given vector field F and the oriented surface S. In other words, find the flux of F across S. in the first octant,
with orientation toward the origin.
(Short Answer)
4.8/5  (38)
(38)
Determine whether F is conservative. If so, find a function f such that .
(Short Answer)
4.8/5  (46)
(46)
Showing 121 - 137 of 137
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)