Exam 7: Section 7: Applications of Integration
Exam 1: Section 1: Preparation for Calculus16 Questions
Exam 1: Section 2: Preparation for Calculus26 Questions
Exam 1: Section 3: Preparation for Calculus23 Questions
Exam 1: Section 4: Preparation for Calculus16 Questions
Exam 1: Section 5: Preparation for Calculus25 Questions
Exam 1: Section 6: Preparation for Calculus8 Questions
Exam 2: Section 1: Limits and Their Properties10 Questions
Exam 2: Section 2: Limits and Their Properties14 Questions
Exam 2: Section 3: Limits and Their Properties25 Questions
Exam 2: Section 4: Limits and Their Properties20 Questions
Exam 2: Section 5 : Limits and Their Properties18 Questions
Exam 3: Section 1 : Differentiation20 Questions
Exam 3: Section 2: Differentiation25 Questions
Exam 3: Section 3: Differentiation26 Questions
Exam 3: Section 4 : Differentiation44 Questions
Exam 3: Section 5: Differentiation30 Questions
Exam 3: Section 6: Differentiation16 Questions
Exam 3: Section 7: Differentiation16 Questions
Exam 3: Section 8: Differentiation12 Questions
Exam 4: Section 1 : Applications of Differentiation19 Questions
Exam 4: Section 2: Applications of Differentiation17 Questions
Exam 4: Section 3: Applications of Differentiation17 Questions
Exam 4: Section 4: Applications of Differentiation26 Questions
Exam 4: Section 5: Applications of Differentiation23 Questions
Exam 4: Section 6: Applications of Differentiation22 Questions
Exam 4: Section 7: Applications of Differentiation15 Questions
Exam 4: Section 8: Applications of Differentiation16 Questions
Exam 4: Section 1: Integration19 Questions
Exam 4: Section 2: Integration17 Questions
Exam 4: Section 3: Integration19 Questions
Exam 4: Section 4: Integration18 Questions
Exam 4: Section 5: Integration31 Questions
Exam 4: Section 6: Integration18 Questions
Exam 4: Section 7: Integration27 Questions
Exam 4: Section 8: Integration16 Questions
Exam 4: Section 9: Integration20 Questions
Exam 6: Section 1: Differential Equations19 Questions
Exam 6: Section 2: Differential Equations25 Questions
Exam 6: Section 3: Differential Equations12 Questions
Exam 6: Section 4: Differential Equations14 Questions
Exam 6: Section 5: Differential Equations17 Questions
Exam 7: Section 1: Applications of Integration18 Questions
Exam 7: Section 2: Applications of Integration18 Questions
Exam 7: Section 3: Applications of Integration17 Questions
Exam 7: Section 4: Applications of Integration18 Questions
Exam 7: Section 5: Applications of Integration16 Questions
Exam 7: Section 6: Applications of Integration19 Questions
Exam 7: Section 7: Applications of Integration15 Questions
Exam 8: Section 1: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 2: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 3: Integration Techniques, Lhôpitals Rule, and Improper Integrals20 Questions
Exam 8: Section 4: Integration Techniques, Lhôpitals Rule, and Improper Integrals19 Questions
Exam 8: Section 5: Integration Techniques, Lhôpitals Rule, and Improper Integrals14 Questions
Exam 8: Section 6: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 7: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 8: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 9: Section 1: Infinite Series17 Questions
Exam 9: Section 2: Infinite Series23 Questions
Exam 9: Section 3: Infinite Series18 Questions
Exam 9: Section 4: Infinite Series21 Questions
Exam 9: Section 5: Infinite Series15 Questions
Exam 9: Section 6: Infinite Series21 Questions
Exam 9: Section 7: Infinite Series18 Questions
Exam 9: Section 8: Infinite Series18 Questions
Exam 9: Section 9: Infinite Series19 Questions
Exam 9: Section 10: Infinite Series16 Questions
Exam 10: Section 1: Conics, Parametric Equations, and Polar Coordinates26 Questions
Exam 10: Section 2: Conics, Parametric Equations, and Polar Coordinates17 Questions
Exam 10: Section 3: Conics, Parametric Equations, and Polar Coordinates22 Questions
Exam 10: Section 4: Conics, Parametric Equations, and Polar Coordinates15 Questions
Exam 10: Section 5: Conics, Parametric Equations, and Polar Coordinates18 Questions
Exam 10: Section 6: Conics, Parametric Equations, and Polar Coordinates19 Questions
Exam 11: Section 1: Vectors and the Geometry of Space20 Questions
Exam 11: Section 2: Vectors and the Geometry of Space21 Questions
Exam 11: Section 3: Vectors and the Geometry of Space18 Questions
Exam 11: Section 4: Vectors and the Geometry of Space18 Questions
Exam 11: Section 5: Vectors and the Geometry of Space21 Questions
Exam 11: Section 6: Vectors and the Geometry of Space20 Questions
Exam 11: Section 7: Vectors and the Geometry of Space19 Questions
Exam 12: Section 1: Vector-Valued Functions21 Questions
Exam 12: Section 2: Vector-Valued Functions24 Questions
Exam 12: Section 3: Vector-Valued Functions18 Questions
Exam 12: Section 4: Vector-Valued Functions20 Questions
Exam 12: Section 5: Vector-Valued Functions19 Questions
Exam 13: Section 1: Functions of Several Variables19 Questions
Exam 13: Section 2: Functions of Several Variables22 Questions
Exam 13: Section 3: Functions of Several Variables23 Questions
Exam 13: Section 4: Functions of Several Variables17 Questions
Exam 13: Section 6: Functions of Several Variables20 Questions
Exam 13: Section 7: Functions of Several Variables20 Questions
Exam 13: Section 8: Functions of Several Variables20 Questions
Exam 13: Section 9: Functions of Several Variables17 Questions
Exam 13: Section 10: Functions of Several Variables18 Questions
Exam 14: Section 1: Multiple Integration20 Questions
Exam 14: Section 2: Multiple Integration19 Questions
Exam 14: Section 3: Multiple Integration20 Questions
Exam 14: Section 4: Multiple Integration18 Questions
Exam 14: Section 5: Multiple Integration18 Questions
Exam 14: Section 6: Multiple Integration19 Questions
Exam 14: Section 7: Multiple Integration19 Questions
Exam 14: Section 8: Multiple Integration19 Questions
Exam 15: Section 1: Vector Analysis21 Questions
Exam 15: Section 2: Vector Analysis18 Questions
Exam 15: Section 3: Vector Analysis18 Questions
Exam 15: Section 4: Vector Analysis18 Questions
Exam 15: Section 5: Vector Analysis21 Questions
Exam 15: Section 6: Vector Analysis18 Questions
Exam 15: Section 7: Vector Analysis18 Questions
Exam 15: Section 8: Vector Analysis17 Questions
Select questions type
Find the fluid force of a triangular vertical plate submerged in water, where the dimensions are given in meters 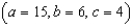 and the weight-density of water is 9800 newtons per cubic meter.
and the weight-density of water is 9800 newtons per cubic meter. 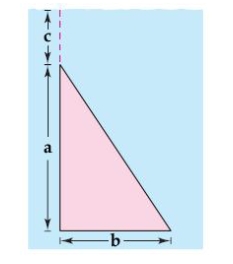
Free
(Multiple Choice)
4.9/5  (40)
(40)
Correct Answer:
A
Find the fluid force of a square vertical plate submerged in water, where 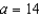 meters and the weight-density of water is 9800 newtons per cubic meter.
meters and the weight-density of water is 9800 newtons per cubic meter. 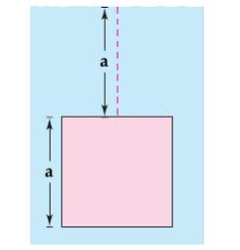
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
C
The area of the top side of a piece of sheet metal is 9 square feet. The sheet metal is submerged horizontally in 8 feet of water. Find the fluid force on the top side. Round your answer to one decimal place.
Free
(Multiple Choice)
4.9/5  (41)
(41)
Correct Answer:
A
The figure is the vertical side of a form for poured concrete that weighs 140.7 pounds per cubic foot. Dimensions in the figure are in feet. Determine force on this part of the concrete form. 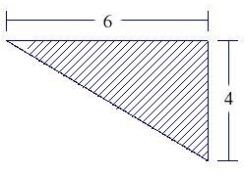
(Multiple Choice)
4.8/5  (35)
(35)
A circular plate of radius r feet is submerged vertically in a tank of fluid that weighs w pounds per cubic foot. The center of the circle is 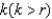 feet below the surface of the fluid. The fluid force on the surface of the plate is given by
feet below the surface of the fluid. The fluid force on the surface of the plate is given by 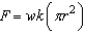 Find the fluid force on the circular plate as shown in the figure given
Find the fluid force on the circular plate as shown in the figure given  feet and
feet and  feet. Round your answer to one decimal place.
feet. Round your answer to one decimal place. 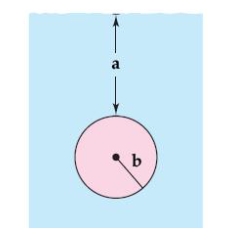
(Multiple Choice)
4.8/5  (36)
(36)
A rectangular plate of height h feet and base b feet is submerged vertically in a tank of fluid that weighs w pounds per cubic foot. The center of the plate is k feet below the surface of the fluid. The fluid force on the surface of the plate is given by 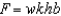 Find the fluid force on the rectangular plate as shown in the figure given
Find the fluid force on the rectangular plate as shown in the figure given 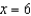 feet and
feet and 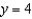 feet. Round your answer to one decimal place.
feet. Round your answer to one decimal place. 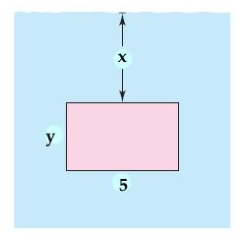
(Multiple Choice)
4.9/5  (38)
(38)
The vertical cross section of an irrigation canal is modeled by 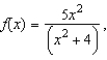 where x is measured in feet and
where x is measured in feet and 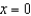 corresponds to the center of the canal. Use the integration capabilities of a graphing utility to approximate the fluid force against a vertical gate used to stop the flow of water if the water is
corresponds to the center of the canal. Use the integration capabilities of a graphing utility to approximate the fluid force against a vertical gate used to stop the flow of water if the water is 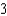 feet deep. Round your answer to three decimal places.
feet deep. Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (32)
(32)
Find the fluid force on the vertical side of the tank, where the dimensions are given in feet. Assume that the tank is full of water. Note: The density of water is 62.4 lbs per cubic foot. 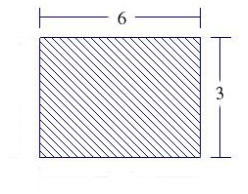
(Multiple Choice)
4.9/5  (32)
(32)
A cylindrical gasoline tank is placed so that the axis of the cylinder is horizontal. Find the fluid force on a circular end of the tank if the tank is full, assuming that the diameter is 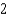 feet and the gasoline weighs
feet and the gasoline weighs 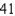 pounds per cubic foot. (Evaluate one integral by a geometric formula and the other by observing that the integrand is an odd function.) Round your answer to two decimal places.
pounds per cubic foot. (Evaluate one integral by a geometric formula and the other by observing that the integrand is an odd function.) Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (31)
(31)
Find the buoyant force of a rectangular solid of the given dimensions submerged in water so that the top side is parallel to the surface of the water. The buoyant force is the difference between the fluid forces on the top and bottom sides of the solid. Round your answer to two decimal places. 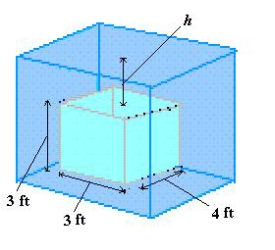
(Multiple Choice)
4.8/5  (32)
(32)
Find the fluid force on the vertical side of the tank, where the dimensions are given in feet. Assume that the tank is full of water. Note: The density of water is 62.4 lbs per cubic foot. 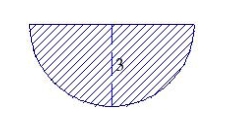
(Multiple Choice)
4.9/5  (39)
(39)
The figure is the vertical side of a form for poured concrete that weighs 140.7 pounds per cubic foot. Dimensions in the figure are in feet. Determine force on this part of the concrete form 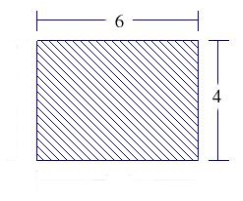
(Multiple Choice)
4.9/5  (32)
(32)
A cylindrical gasoline tank is placed so that the axis of the cylinder is horizontal. Find the fluid force on a circular end of the tank if the tank is half full, assuming that the diameter is 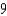 feet and the gasoline weighs 42 pounds per cubic foot.
feet and the gasoline weighs 42 pounds per cubic foot.
(Multiple Choice)
4.8/5  (38)
(38)
Find the fluid force on the vertical side of the tank, where the dimensions are given in feet. Assume that the tank is full of water. Note: The density of water is 62.4 lbs per cubic foot. 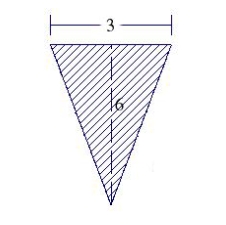
(Multiple Choice)
4.8/5  (31)
(31)
A porthole on a vertical side of a submarine (submerged in seawater) is 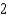 square
square 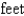 . Find the fluid force on the porthole, assuming that the center of the square is
. Find the fluid force on the porthole, assuming that the center of the square is 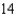 feet below the surface.
feet below the surface.
(Multiple Choice)
4.8/5  (36)
(36)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)