Explore all topics
Start Free Trial
Need Help? Contact us
back arrowfull exam logo
search
ai logoChat with AI
Servicesarrow
Discoverarrow

Topics

Explore all topics
Discover more topics

Exam 5: Regression With a Single Regressor: Hypothesis Tests and Confidence Intervals

arrow
Exam 1: Economic Questions and Data17 Questionsadd course
Exam 2: Review of Probability71 Questionsadd course
Exam 3: Review of Statistics63 Questionsadd course
Exam 4: Linear Regression With One Regressor65 Questionsadd course
Exam 5: Regression With a Single Regressor: Hypothesis Tests and Confidence Intervals59 Questionsadd course
Exam 6: Linear Regression With Multiple Regressors65 Questionsadd course
Exam 7: Hypothesis Tests and Confidence Intervals in Multiple Regression65 Questionsadd course
Exam 8: Nonlinear Regression Functions62 Questionsadd course
Exam 9: Assessing Studies Based on Multiple Regression65 Questionsadd course
Exam 10: Regression With Panel Data50 Questionsadd course
Exam 11: Regression With a Binary Dependent Variable50 Questionsadd course
Exam 12: Instrumental Variables Regression50 Questionsadd course
Exam 13: Experiments and Quasi-Experiments50 Questionsadd course
Exam 14: Introduction to Time Series Regression and Forecasting50 Questionsadd course
Exam 15: Estimation of Dynamic Causal Effects50 Questionsadd course
Exam 16: Additional Topics in Time Series Regression50 Questionsadd course
Exam 17: The Theory of Linear Regression With One Regressor49 Questionsadd course
Exam 18: The Theory of Multiple Regression50 Questionsadd course
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags
search iconSearch Question
flashcardsStudy Flashcards
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags

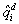Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient.Briefly justify your decision. (a) Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient.Briefly justify your decision. (a) = 0 + 1pi,where qd is the quantity demanded for a good,and p is its price. (b) = 0 + 1 ,where is the actual house price,and is the assessed house price.You want to test whether or not the assessment is correct,on average. (c) i = 0 + 1 ,where C is household consumption,and Yd is personal disposable income. 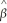= Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient.Briefly justify your decision. (a) = 0 + 1pi,where qd is the quantity demanded for a good,and p is its price. (b) = 0 + 1 ,where is the actual house price,and is the assessed house price.You want to test whether or not the assessment is correct,on average. (c) i = 0 + 1 ,where C is household consumption,and Yd is personal disposable income. 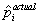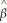0 + Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient.Briefly justify your decision. (a) = 0 + 1pi,where qd is the quantity demanded for a good,and p is its price. (b) = 0 + 1 ,where is the actual house price,and is the assessed house price.You want to test whether or not the assessment is correct,on average. (c) i = 0 + 1 ,where C is household consumption,and Yd is personal disposable income. 1pi,where qd is the quantity demanded for a good,and p is its price. 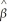(b) Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient.Briefly justify your decision. (a) = 0 + 1pi,where qd is the quantity demanded for a good,and p is its price. (b) = 0 + 1 ,where is the actual house price,and is the assessed house price.You want to test whether or not the assessment is correct,on average. (c) i = 0 + 1 ,where C is household consumption,and Yd is personal disposable income. 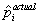= Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient.Briefly justify your decision. (a) = 0 + 1pi,where qd is the quantity demanded for a good,and p is its price. (b) = 0 + 1 ,where is the actual house price,and is the assessed house price.You want to test whether or not the assessment is correct,on average. (c) i = 0 + 1 ,where C is household consumption,and Yd is personal disposable income. 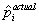0 + Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient.Briefly justify your decision. (a) = 0 + 1pi,where qd is the quantity demanded for a good,and p is its price. (b) = 0 + 1 ,where is the actual house price,and is the assessed house price.You want to test whether or not the assessment is correct,on average. (c) i = 0 + 1 ,where C is household consumption,and Yd is personal disposable income. 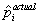1 Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient.Briefly justify your decision. (a) = 0 + 1pi,where qd is the quantity demanded for a good,and p is its price. (b) = 0 + 1 ,where is the actual house price,and is the assessed house price.You want to test whether or not the assessment is correct,on average. (c) i = 0 + 1 ,where C is household consumption,and Yd is personal disposable income. 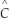,where Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient.Briefly justify your decision. (a) = 0 + 1pi,where qd is the quantity demanded for a good,and p is its price. (b) = 0 + 1 ,where is the actual house price,and is the assessed house price.You want to test whether or not the assessment is correct,on average. (c) i = 0 + 1 ,where C is household consumption,and Yd is personal disposable income. 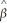is the actual house price,and Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient.Briefly justify your decision. (a) = 0 + 1pi,where qd is the quantity demanded for a good,and p is its price. (b) = 0 + 1 ,where is the actual house price,and is the assessed house price.You want to test whether or not the assessment is correct,on average. (c) i = 0 + 1 ,where C is household consumption,and Yd is personal disposable income. is the assessed house price.You want to test whether or not the assessment is correct,on average. (c) Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient.Briefly justify your decision. (a) = 0 + 1pi,where qd is the quantity demanded for a good,and p is its price. (b) = 0 + 1 ,where is the actual house price,and is the assessed house price.You want to test whether or not the assessment is correct,on average. (c) i = 0 + 1 ,where C is household consumption,and Yd is personal disposable income. i = Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient.Briefly justify your decision. (a) = 0 + 1pi,where qd is the quantity demanded for a good,and p is its price. (b) = 0 + 1 ,where is the actual house price,and is the assessed house price.You want to test whether or not the assessment is correct,on average. (c) i = 0 + 1 ,where C is household consumption,and Yd is personal disposable income. 0 + Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient.Briefly justify your decision. (a) = 0 + 1pi,where qd is the quantity demanded for a good,and p is its price. (b) = 0 + 1 ,where is the actual house price,and is the assessed house price.You want to test whether or not the assessment is correct,on average. (c) i = 0 + 1 ,where C is household consumption,and Yd is personal disposable income. 1 Below you are asked to decide on whether or not to use a one-sided alternative or a two-sided alternative hypothesis for the slope coefficient.Briefly justify your decision. (a) = 0 + 1pi,where qd is the quantity demanded for a good,and p is its price. (b) = 0 + 1 ,where is the actual house price,and is the assessed house price.You want to test whether or not the assessment is correct,on average. (c) i = 0 + 1 ,where C is household consumption,and Yd is personal disposable income. ,where C is household consumption,and Yd is personal disposable income.

(Essay)
4.8/5
(40)
Question 41

If the errors are heteroskedastic,then

(Multiple Choice)
4.8/5
(33)
Question 42

(Requires Appendix material from Chapters 4 and 5)Shortly before you are making a group presentation on the testscore/student-teacher ratio results,you realize that one of your peers forgot to type all the relevant information on one of your slides.Here is what you see: (Requires Appendix material from Chapters 4 and 5)Shortly before you are making a group presentation on the testscore/student-teacher ratio results,you realize that one of your peers forgot to type all the relevant information on one of your slides.Here is what you see: 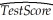= 698.9 - STR,R2 = 0.051,SER = 18.6 (9.47)(0.48) In addition,your group member explains that he ran the regression in a standard spreadsheet program,and that,as a result,the standard errors in parenthesis are homoskedasticity-only standard errors. (a)Find the value for the slope coefficient. (b)Calculate the t-statistic for the slope and the intercept.Test the hypothesis that the intercept and the slope are different from zero. (c)Should you be concerned that your group member only gave you the result for the homoskedasticity-only standard error formula,instead of using the heteroskedasticity-robust standard errors? = 698.9 - STR,R2 = 0.051,SER = 18.6 (9.47)(0.48) In addition,your group member explains that he ran the regression in a standard spreadsheet program,and that,as a result,the standard errors in parenthesis are homoskedasticity-only standard errors. (a)Find the value for the slope coefficient. (b)Calculate the t-statistic for the slope and the intercept.Test the hypothesis that the intercept and the slope are different from zero. (c)Should you be concerned that your group member only gave you the result for the homoskedasticity-only standard error formula,instead of using the heteroskedasticity-robust standard errors?

(Essay)
4.7/5
(34)
Question 43

You extract approximately 5,000 observations from the Current Population Survey (CPS)and estimate the following regression function: You extract approximately 5,000 observations from the Current Population Survey (CPS)and estimate the following regression function: = 3.32 - 0.45 Age,R2= 0.02,SER = 8.66 (1.00)(0.04) Where ahe is average hourly earnings,and Age is the individual's age.Given the specification,your 95% confidence interval for the effect of changing age by 5 years is approximately = 3.32 - 0.45 You extract approximately 5,000 observations from the Current Population Survey (CPS)and estimate the following regression function: = 3.32 - 0.45 Age,R2= 0.02,SER = 8.66 (1.00)(0.04) Where ahe is average hourly earnings,and Age is the individual's age.Given the specification,your 95% confidence interval for the effect of changing age by 5 years is approximately Age,R2= 0.02,SER = 8.66 (1.00)(0.04) Where ahe is average hourly earnings,and Age is the individual's age.Given the specification,your 95% confidence interval for the effect of changing age by 5 years is approximately

(Multiple Choice)
4.9/5
(34)
Question 44

Assume that the homoskedastic normal regression assumption hold.Using the Student t-distribution,find the critical value for the following situation: (a)n = 28,5% significance level,one-sided test. (b)n = 40,1% significance level,two-sided test. (c)n = 10,10% significance level,one-sided test. (d)n = ∞,5% significance level,two-sided test.

(Essay)
4.8/5
(29)
Question 45

Carefully discuss the advantages of using heteroskedasticity-robust standard errors over standard errors calculated under the assumption of homoskedasticity.Give at least five examples where it is very plausible to assume that the errors display heteroskedasticity.

(Essay)
4.8/5
(36)
Question 46

Consider the following regression line: Consider the following regression line: = 698.9 - 2.28 × STR.You are told that the t-statistic on the slope coefficient is 4.38.What is the standard error of the slope coefficient? = 698.9 - 2.28 × STR.You are told that the t-statistic on the slope coefficient is 4.38.What is the standard error of the slope coefficient?

(Multiple Choice)
4.8/5
(37)
Question 47

Imagine that you were told that the t-statistic for the slope coefficient of the regression line 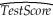Imagine that you were told that the t-statistic for the slope coefficient of the regression line = 698.9 - 2.28 × STR was 4.38.What are the units of measurement for the t-statistic? = 698.9 - 2.28 × STR was 4.38.What are the units of measurement for the t-statistic?

(Multiple Choice)
4.8/5
(33)
Question 48

(Requires Appendix material and Calculus)Equation (5.36)in your textbook derives the conditional variance for any old conditionally unbiased estimator (Requires Appendix material and Calculus)Equation (5.36)in your textbook derives the conditional variance for any old conditionally unbiased estimator 1 to be var( 1 X1,... ,Xn)= where the conditions for conditional unbiasedness are = 0 and = 1.As an alternative to the BLUE proof presented in your textbook,you recall from one of your calculus courses that you could minimize the variance subject to the two constraints,thereby making the variance as small as possible while the constraints are holding.Show that in doing so you get the OLS weights .(You may assume that X1,... ,Xn are nonrandom (fixed over repeated samples). ) 1 to be var( (Requires Appendix material and Calculus)Equation (5.36)in your textbook derives the conditional variance for any old conditionally unbiased estimator 1 to be var( 1 X1,... ,Xn)= where the conditions for conditional unbiasedness are = 0 and = 1.As an alternative to the BLUE proof presented in your textbook,you recall from one of your calculus courses that you could minimize the variance subject to the two constraints,thereby making the variance as small as possible while the constraints are holding.Show that in doing so you get the OLS weights .(You may assume that X1,... ,Xn are nonrandom (fixed over repeated samples). ) 1 (Requires Appendix material and Calculus)Equation (5.36)in your textbook derives the conditional variance for any old conditionally unbiased estimator 1 to be var( 1 X1,... ,Xn)= where the conditions for conditional unbiasedness are = 0 and = 1.As an alternative to the BLUE proof presented in your textbook,you recall from one of your calculus courses that you could minimize the variance subject to the two constraints,thereby making the variance as small as possible while the constraints are holding.Show that in doing so you get the OLS weights .(You may assume that X1,... ,Xn are nonrandom (fixed over repeated samples). ) X1,... ,Xn)= (Requires Appendix material and Calculus)Equation (5.36)in your textbook derives the conditional variance for any old conditionally unbiased estimator 1 to be var( 1 X1,... ,Xn)= where the conditions for conditional unbiasedness are = 0 and = 1.As an alternative to the BLUE proof presented in your textbook,you recall from one of your calculus courses that you could minimize the variance subject to the two constraints,thereby making the variance as small as possible while the constraints are holding.Show that in doing so you get the OLS weights .(You may assume that X1,... ,Xn are nonrandom (fixed over repeated samples). ) where the conditions for conditional unbiasedness are (Requires Appendix material and Calculus)Equation (5.36)in your textbook derives the conditional variance for any old conditionally unbiased estimator 1 to be var( 1 X1,... ,Xn)= where the conditions for conditional unbiasedness are = 0 and = 1.As an alternative to the BLUE proof presented in your textbook,you recall from one of your calculus courses that you could minimize the variance subject to the two constraints,thereby making the variance as small as possible while the constraints are holding.Show that in doing so you get the OLS weights .(You may assume that X1,... ,Xn are nonrandom (fixed over repeated samples). ) = 0 and (Requires Appendix material and Calculus)Equation (5.36)in your textbook derives the conditional variance for any old conditionally unbiased estimator 1 to be var( 1 X1,... ,Xn)= where the conditions for conditional unbiasedness are = 0 and = 1.As an alternative to the BLUE proof presented in your textbook,you recall from one of your calculus courses that you could minimize the variance subject to the two constraints,thereby making the variance as small as possible while the constraints are holding.Show that in doing so you get the OLS weights .(You may assume that X1,... ,Xn are nonrandom (fixed over repeated samples). ) = 1.As an alternative to the BLUE proof presented in your textbook,you recall from one of your calculus courses that you could minimize the variance subject to the two constraints,thereby making the variance as small as possible while the constraints are holding.Show that in doing so you get the OLS weights 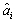(Requires Appendix material and Calculus)Equation (5.36)in your textbook derives the conditional variance for any old conditionally unbiased estimator 1 to be var( 1 X1,... ,Xn)= where the conditions for conditional unbiasedness are = 0 and = 1.As an alternative to the BLUE proof presented in your textbook,you recall from one of your calculus courses that you could minimize the variance subject to the two constraints,thereby making the variance as small as possible while the constraints are holding.Show that in doing so you get the OLS weights .(You may assume that X1,... ,Xn are nonrandom (fixed over repeated samples). ) .(You may assume that X1,... ,Xn are nonrandom (fixed over repeated samples). )

(Essay)
4.9/5
(39)
Question 49

In general,the t-statistic has the following form:

(Multiple Choice)
4.8/5
(38)
Question 50

The construction of the t-statistic for a one- and a two-sided hypothesis

(Multiple Choice)
4.9/5
(39)
Question 51

The proof that OLS is BLUE requires all of the following assumptions with the exception of:

(Multiple Choice)
4.9/5
(40)
Question 52

Let Let be distributed N(0, ),i.e. ,the errors are distributed normally with a constant variance (homoskedasticity).This results in being distributed N(β1, ),where .Statistical inference would be straightforward if was known.One way to deal with this problem is to replace with an estimator .Clearly since this introduces more uncertainty,you cannot expect to be still normally distributed.Indeed,the t-statistic now follows Student's t distribution.Look at the table for the Student t-distribution and focus on the 5% two-sided significance level.List the critical values for 10 degrees of freedom,30 degrees of freedom,60 degrees of freedom,and finally ∞ degrees of freedom.Describe how the notion of uncertainty about can be incorporated about the tails of the t-distribution as the degrees of freedom increase. be distributed N(0, Let 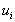be distributed N(0, ),i.e. ,the errors are distributed normally with a constant variance (homoskedasticity).This results in being distributed N(β1, ),where .Statistical inference would be straightforward if was known.One way to deal with this problem is to replace with an estimator .Clearly since this introduces more uncertainty,you cannot expect to be still normally distributed.Indeed,the t-statistic now follows Student's t distribution.Look at the table for the Student t-distribution and focus on the 5% two-sided significance level.List the critical values for 10 degrees of freedom,30 degrees of freedom,60 degrees of freedom,and finally ∞ degrees of freedom.Describe how the notion of uncertainty about can be incorporated about the tails of the t-distribution as the degrees of freedom increase. ),i.e. ,the errors are distributed normally with a constant variance (homoskedasticity).This results in Let be distributed N(0, ),i.e. ,the errors are distributed normally with a constant variance (homoskedasticity).This results in being distributed N(β1, ),where .Statistical inference would be straightforward if was known.One way to deal with this problem is to replace with an estimator .Clearly since this introduces more uncertainty,you cannot expect to be still normally distributed.Indeed,the t-statistic now follows Student's t distribution.Look at the table for the Student t-distribution and focus on the 5% two-sided significance level.List the critical values for 10 degrees of freedom,30 degrees of freedom,60 degrees of freedom,and finally ∞ degrees of freedom.Describe how the notion of uncertainty about can be incorporated about the tails of the t-distribution as the degrees of freedom increase. 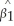being distributed N(β1, Let be distributed N(0, ),i.e. ,the errors are distributed normally with a constant variance (homoskedasticity).This results in being distributed N(β1, ),where .Statistical inference would be straightforward if was known.One way to deal with this problem is to replace with an estimator .Clearly since this introduces more uncertainty,you cannot expect to be still normally distributed.Indeed,the t-statistic now follows Student's t distribution.Look at the table for the Student t-distribution and focus on the 5% two-sided significance level.List the critical values for 10 degrees of freedom,30 degrees of freedom,60 degrees of freedom,and finally ∞ degrees of freedom.Describe how the notion of uncertainty about can be incorporated about the tails of the t-distribution as the degrees of freedom increase. 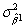),where Let be distributed N(0, ),i.e. ,the errors are distributed normally with a constant variance (homoskedasticity).This results in being distributed N(β1, ),where .Statistical inference would be straightforward if was known.One way to deal with this problem is to replace with an estimator .Clearly since this introduces more uncertainty,you cannot expect to be still normally distributed.Indeed,the t-statistic now follows Student's t distribution.Look at the table for the Student t-distribution and focus on the 5% two-sided significance level.List the critical values for 10 degrees of freedom,30 degrees of freedom,60 degrees of freedom,and finally ∞ degrees of freedom.Describe how the notion of uncertainty about can be incorporated about the tails of the t-distribution as the degrees of freedom increase. 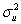.Statistical inference would be straightforward if Let be distributed N(0, ),i.e. ,the errors are distributed normally with a constant variance (homoskedasticity).This results in being distributed N(β1, ),where .Statistical inference would be straightforward if was known.One way to deal with this problem is to replace with an estimator .Clearly since this introduces more uncertainty,you cannot expect to be still normally distributed.Indeed,the t-statistic now follows Student's t distribution.Look at the table for the Student t-distribution and focus on the 5% two-sided significance level.List the critical values for 10 degrees of freedom,30 degrees of freedom,60 degrees of freedom,and finally ∞ degrees of freedom.Describe how the notion of uncertainty about can be incorporated about the tails of the t-distribution as the degrees of freedom increase. was known.One way to deal with this problem is to replace Let be distributed N(0, ),i.e. ,the errors are distributed normally with a constant variance (homoskedasticity).This results in being distributed N(β1, ),where .Statistical inference would be straightforward if was known.One way to deal with this problem is to replace with an estimator .Clearly since this introduces more uncertainty,you cannot expect to be still normally distributed.Indeed,the t-statistic now follows Student's t distribution.Look at the table for the Student t-distribution and focus on the 5% two-sided significance level.List the critical values for 10 degrees of freedom,30 degrees of freedom,60 degrees of freedom,and finally ∞ degrees of freedom.Describe how the notion of uncertainty about can be incorporated about the tails of the t-distribution as the degrees of freedom increase. with an estimator Let be distributed N(0, ),i.e. ,the errors are distributed normally with a constant variance (homoskedasticity).This results in being distributed N(β1, ),where .Statistical inference would be straightforward if was known.One way to deal with this problem is to replace with an estimator .Clearly since this introduces more uncertainty,you cannot expect to be still normally distributed.Indeed,the t-statistic now follows Student's t distribution.Look at the table for the Student t-distribution and focus on the 5% two-sided significance level.List the critical values for 10 degrees of freedom,30 degrees of freedom,60 degrees of freedom,and finally ∞ degrees of freedom.Describe how the notion of uncertainty about can be incorporated about the tails of the t-distribution as the degrees of freedom increase. .Clearly since this introduces more uncertainty,you cannot expect Let be distributed N(0, ),i.e. ,the errors are distributed normally with a constant variance (homoskedasticity).This results in being distributed N(β1, ),where .Statistical inference would be straightforward if was known.One way to deal with this problem is to replace with an estimator .Clearly since this introduces more uncertainty,you cannot expect to be still normally distributed.Indeed,the t-statistic now follows Student's t distribution.Look at the table for the Student t-distribution and focus on the 5% two-sided significance level.List the critical values for 10 degrees of freedom,30 degrees of freedom,60 degrees of freedom,and finally ∞ degrees of freedom.Describe how the notion of uncertainty about can be incorporated about the tails of the t-distribution as the degrees of freedom increase. to be still normally distributed.Indeed,the t-statistic now follows Student's t distribution.Look at the table for the Student t-distribution and focus on the 5% two-sided significance level.List the critical values for 10 degrees of freedom,30 degrees of freedom,60 degrees of freedom,and finally ∞ degrees of freedom.Describe how the notion of uncertainty about Let be distributed N(0, ),i.e. ,the errors are distributed normally with a constant variance (homoskedasticity).This results in being distributed N(β1, ),where .Statistical inference would be straightforward if was known.One way to deal with this problem is to replace with an estimator 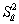.Clearly since this introduces more uncertainty,you cannot expect 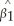to be still normally distributed.Indeed,the t-statistic now follows Student's t distribution.Look at the table for the Student t-distribution and focus on the 5% two-sided significance level.List the critical values for 10 degrees of freedom,30 degrees of freedom,60 degrees of freedom,and finally ∞ degrees of freedom.Describe how the notion of uncertainty about can be incorporated about the tails of the t-distribution as the degrees of freedom increase. can be incorporated about the tails of the t-distribution as the degrees of freedom increase.

(Essay)
4.9/5
(36)
Question 53

In the presence of heteroskedasticity,and assuming that the usual least squares assumptions hold,the OLS estimator is

(Multiple Choice)
4.8/5
(36)
Question 54

Heteroskedasticity means that

(Multiple Choice)
4.8/5
(33)
Question 55

Using the California School data set from your textbook,you run the following regression: Using the California School data set from your textbook,you run the following regression: = 698.9 - 2.28 STR n = 420,SER = 9.4 where TestScore is the average test score in the district and STR is the student-teacher ratio.The sample standard deviation of test scores is 19.05,and the sample standard deviation of the student teacher ratio is 1.89. a. Find the regression R2 and the correlation coefficient between test scores and the student teacher ratio. b. Find the homoskedasticity-only standard error of the slope. = 698.9 - 2.28 STR n = 420,SER = 9.4 where TestScore is the average test score in the district and STR is the student-teacher ratio.The sample standard deviation of test scores is 19.05,and the sample standard deviation of the student teacher ratio is 1.89. a. Find the regression R2 and the correlation coefficient between test scores and the student teacher ratio. b. Find the homoskedasticity-only standard error of the slope.

(Essay)
4.8/5
(32)
Question 56

You have collected 14,925 observations from the Current Population Survey.There are 6,285 females in the sample,and 8,640 males.The females report a mean of average hourly earnings of $16.50 with a standard deviation of $9.06.The males have an average of $20.09 and a standard deviation of $10.85.The overall mean average hourly earnings is $18.58. a.Using the t-statistic for testing differences between two means (section 3.4 of your textbook),decide whether or not there is sufficient evidence to reject the null hypothesis that females and males have identical average hourly earnings. b.You decide to run two regressions: first,you simply regress average hourly earnings on an intercept only.Next,you repeat this regression,but only for the 6,285 females in the sample.What will the regression coefficients be in each of the two regressions? c.Finally you run a regression over the entire sample of average hourly earnings on an intercept and a binary variable DFemme,where this variable takes on a value of 1 if the individual is a female,and is 0 otherwise.What will be the value of the intercept? What will be the value of the coefficient of the binary variable? d.What is the standard error on the slope coefficient? What is the t-statistic? e.Had you used the homoskedasticity-only standard error in (d)and calculated the t-statistic,how would you have had to change the test-statistic in (a)to get the identical result?

(Essay)
4.9/5
(42)
Question 57

One of the following steps is not required as a step to test for the null hypothesis:

(Multiple Choice)
4.9/5
(37)
Question 58

You have obtained measurements of height in inches of 29 female and 81 male students (Studenth)at your university.A regression of the height on a constant and a binary variable (BFemme),which takes a value of one for females and is zero otherwise,yields the following result: You have obtained measurements of height in inches of 29 female and 81 male students (Studenth)at your university.A regression of the height on a constant and a binary variable (BFemme),which takes a value of one for females and is zero otherwise,yields the following result: 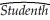= 71.0 - 4.84×BFemme ,R2 = 0.40,SER = 2.0 (0.3)(0.57) (a)What is the interpretation of the intercept? What is the interpretation of the slope? How tall are females,on average? (b)Test the hypothesis that females,on average,are shorter than males,at the 1% level. (c)Is it likely that the error term is homoskedastic here? = 71.0 - 4.84×BFemme ,R2 = 0.40,SER = 2.0 (0.3)(0.57) (a)What is the interpretation of the intercept? What is the interpretation of the slope? How tall are females,on average? (b)Test the hypothesis that females,on average,are shorter than males,at the 1% level. (c)Is it likely that the error term is homoskedastic here?

(Essay)
4.8/5
(37)
Question 59
Showing 41 - 59 of 59
close modal

Filters

  • Essay(0)
  • Multiple Choice(0)
  • Short Answer(0)
  • True False(0)
  • Matching(0)