Exam 15: Optimization- Local and Global Extrema
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
What do the second derivatives tell you about the graph of Select all that apply.
(Multiple Choice)
4.7/5  (32)
(32)
Let .
There exist values of a and b so that takes a minimum value of 8 on the unit circle at the point .
(True/False)
4.8/5  (35)
(35)
Suppose the quantity, q, of a good produced depends on the number of workers, w, and the amount of capital, k, invested and is represented by the Cobb-Douglas function .In addition, labor costs are $20 per worker and capital costs are $20 per unit, and the budget is $3680.Using Lagrange multipliers, find the optimum number of units of capital.
(Short Answer)
4.8/5  (28)
(28)
Consider the function Determine all the local maximum, minimum and saddle points in the region
(Short Answer)
4.8/5  (43)
(43)
Suppose that Find a normal vector to the tangent plane of f at the point (1, 1).Select all that apply.
(Multiple Choice)
4.8/5  (35)
(35)
Consider the four points A = (1, 0), B = (2, 3), C = (3, 5)and D = (4, 3)in the xy-plane.
Find the values of a, b and c to determine the parabola of best fit, for these points.
(The parabola of best fit minimizes the sum of the squares of the vertical distances from each point to the parabola.)
(Essay)
4.8/5  (25)
(25)
Find three positive numbers whose product is 11 and whose sum is a minimum.What is the minimum sum?
(Essay)
4.8/5  (29)
(29)
Level curves of f(x, y)are shown in the figure below.(Darker shades indicate regions with lower levels.)
Determine if is positive, negative or zero. 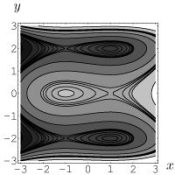
(Essay)
4.8/5  (32)
(32)
The owner of a jewelry store has to decide how to allocate a budget of $540,000.He notices that the earnings of the company depend on investment in inventory x1 (in thousands of dollars)and expenditure x2 on advertising (in thousands of dollars)according to the function How should the owner allocate the $540,000 between inventory and advertising to maximize his profit?
(Essay)
4.9/5  (27)
(27)
A zoo is designing a giant bird cage consisting of a cylinder of radius r feet and height h feet with a hemisphere on top (no bottom).The material for the hemisphere costs $20 per square foot and the material for the cylindrical sides costs $10 per square foot; the zoo has a budget of $5120.Find the values of r and h giving the birds the greatest space inside assuming the zoo stays within its budget.
(Essay)
4.7/5  (27)
(27)
Let Determine all local maxima, minima, and saddle points.Are the local extrema also global extrema?
(Short Answer)
4.9/5  (38)
(38)
Suppose that (0, -2)is a critical point of a smooth function f(x, y)with What can you conclude about the behavior of the function f near (0, -2)?
(Essay)
4.9/5  (43)
(43)
Let .Let satisfy .Explain why the maximum of f subject to the constraint cannot occur at the point .
(Essay)
4.8/5  (39)
(39)
Suppose that Find an equation of the tangent plane to the graph of f at the point (2, 2).
(Multiple Choice)
4.9/5  (35)
(35)
A company manufactures a product using x, y and z units of three different raw materials.The quantity produced is given by The production is described by the function .Suppose the cost of the materials per unit is $20, $15 and $24 respectively.
(a)Find the cheapest way to produce 6300 units of the product.
(b)Find the value of in and interpret this value.
(Essay)
4.8/5  (28)
(28)
Showing 61 - 77 of 77
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)