Exam 15: Optimization- Local and Global Extrema
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
It can be shown that are the critical points of the function .Which of the following are classified correctly? Select all that apply.
(Multiple Choice)
4.9/5  (35)
(35)
The Lagrange multipliers needed to find the maximum and minimum values of 8xy on the circle is , where .Estimate the maximum and minimum values of 8xy subject to the constraint .
(Essay)
4.8/5  (31)
(31)
Find the maximum and minimum values of the function subject to the constraint .
(Short Answer)
4.8/5  (27)
(27)
The temperature at each point in the first quadrant is given by .Find the hottest point in the first quadrant and determine its temperature.
(Essay)
4.7/5  (34)
(34)
A company has two manufacturing plants which manufacture the same item.Suppose the cost function is given by where q1 and q2 are the quantities (measured in thousands)produced in each plant.The total demand q1 + q2 is related to the price, p, by How much should each plant produce in order to maximize the company's profit?
(Essay)
4.8/5  (34)
(34)
Find the critical points of and classify each as maximum, minimum or saddle.
(Essay)
4.7/5  (35)
(35)
Without calculating the discriminant, explain using the contour diagram for why f has a saddle point at (0, 0). 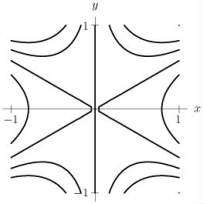
(Essay)
4.7/5  (33)
(33)
Let Which figure best represents the level curves of this function?
(Multiple Choice)
4.8/5  (47)
(47)
A coffee company sells three brands of coffee.Brand A costs p1 dollars per can, brand B costs p2 dollars per can, and brand C costs p3 dollars per can.The demand (in hundreds of cans)depends on the prices as follows:
demand for brand A ,
demand for brand B ,
demand for brand C .
The company can produce 69,000 cans.What selling prices optimize the total revenue?
(Essay)
4.7/5  (40)
(40)
The function f(x, y)has a local maximum at (-1, 1). What can you say (if anything)about the values of ?
(Multiple Choice)
4.9/5  (37)
(37)
Determine the nature of the critical points of the function
(Multiple Choice)
4.9/5  (36)
(36)
The function has a saddle point at (-1, 12).Which of the following is a sketch of the level curves of f near this point?
(Multiple Choice)
4.7/5  (28)
(28)
Let , where a, b are any numbers with a 2.
Find the critical point of f.(Express your answer in terms of the constants a and b.)
(Essay)
4.7/5  (37)
(37)
The Green Leaf Bakery makes two types of chocolate cakes, Delicious and Extra Delicious.Each Delicious requires 0.1 lb of European chocolate, while each Extra Delicious requires 0.2 lb.Currently there are only 233 lb of chocolate available each month.Suppose the profit function is given by: where x is the number of Delicious cakes and y is the number of Extra Delicious cakes that the bakery produces each month.
(a)How many of each cake should the bakery produce each month to maximize profit?
(b)What is the value of in part (a)(if )? What does it mean?
(c)It will cost $19.00 to get an extra pound of European chocolate.Should the bakery buy it?
(Essay)
4.8/5  (29)
(29)
Find all the critical points of the function Classify these critical points as local maxima, local minima, or saddle points.
(Short Answer)
4.8/5  (27)
(27)
Let where k 0.Determine the values of k (if any)for which the critical point at (-1, 0)is a local minimum.
(Essay)
4.8/5  (30)
(30)
Showing 41 - 60 of 77
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)