Exam 15: Optimization- Local and Global Extrema
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
The contour diagram of f is shown below.Which of the points A, B, C, D, and E appear to be critical points? Select all that apply. 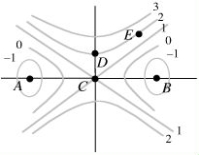
(Multiple Choice)
4.7/5  (25)
(25)
The Perfect House company produces two types of bathtub, the Hydro Deluxe model and the Singing Bird model.The company noticed that demand and prices are related.In particular,
for Hydro Deluxe: demand = 1900 - price of Hydro Deluxe + price of Singing Bird
for Singing Bird: demand = 1450 + price of Hydro Deluxe -2(price of Singing Bird).
The costs of manufacturing the Hydro Deluxe and Singing Bird are $500 and $300 per unit respectively.Determine the price of each model that gives the maximum profit.
(Essay)
4.9/5  (22)
(22)
Level curves of f(x, y)are shown in the figure below.(Darker shades indicate regions with lower levels.) Is the point (-1, 2)a local maximum, a local minimum, or a saddle point of f, or is it none of these? 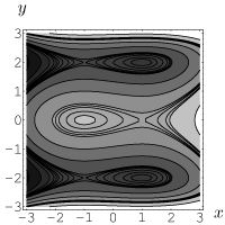
(Multiple Choice)
4.9/5  (34)
(34)
Suppose that Find the minimum value of the function f when (x,y)is constrained to lie on or inside the triangle with vertices (0,-2), (0,1), and (1,-2).Give your answer to 4 decimal places.
(Essay)
4.9/5  (36)
(36)
Suppose that (1, -4)is a critical point of a smooth function f(x, y)with Find the quadratic approximation of f at (1, -4).
(Essay)
4.9/5  (37)
(37)
Find the critical points of Do this by setting and optimizing subject to the constraint
(Essay)
4.8/5  (40)
(40)
The following results are obtained when optimizing f(x, y)subject to the constraint g(x, y)= 39.The maximum value is f(5, 7)= 42, the Lagrange multiplier = 3 (when )and .If the constraint condition is changed to g(x, y)= 40, what will be new maximum value of f(x, y)?
(Essay)
4.8/5  (36)
(36)
Consider the four points A = (1, 0), B = (2, 2), C = (3, 5)and D = (4, 3)in the xy-plane.
Find a and b in the line of best fit y = ax + b for these points.
(The line of best fit minimizes the sum of the squares of the vertical distances from each point to the line.)
(Essay)
4.7/5  (34)
(34)
The point (-2, 1)is a critical point of Classify it either as a local minimum, local maximum, or saddle point.
(Short Answer)
4.9/5  (33)
(33)
Determine three positive numbers x, y, z that maximize under the condition x + y + z = 17.
(Essay)
4.8/5  (31)
(31)
If C is a circle in the plane, and if f(x, y)is differentiable and is not constant when constrained to C, then there must be at least one point on C where is perpendicular to C.
(True/False)
4.8/5  (36)
(36)
Let .Find values of a and b so that takes a maximum value of 4 on the unit circle at the point .
(Essay)
4.8/5  (44)
(44)
The following results are obtained when optimizing f(x, y)subject to the constraint g(x, y)= 35.The maximum value is f(5, 7)= 39, the Lagrange multiplier = 4 (when )and .What is g(5, 7)?
(Essay)
4.8/5  (33)
(33)
A company manufactures a product using x, y and z units of three different raw materials.The quantity produced is given by the function .Suppose the cost of the materials per unit is $20, $25 and $75 respectively.
Find the maximum production if the budget is limited to $6000.
(Essay)
4.9/5  (33)
(33)
Let in the square S bounded by .Then is a critical point.What kind of critical point is it?
(Multiple Choice)
4.8/5  (25)
(25)
Let , for constants a, b, c, and d, with .
The constants can be chosen in such a way that f will have a local minimum.
(True/False)
4.7/5  (33)
(33)
An exam question asks students to find the maximum of on the circle , and the gradient vectors of f and g at that point.A student gave the following
(Essay)
4.9/5  (30)
(30)
Suppose that Find and classify (as local maxima, minima, or saddle points)all critical points of f.
(Essay)
4.8/5  (32)
(32)
Consider the function Check that (0,0)is a critical point of f and classify it as a local minimum, local maximum or saddle point.
(Short Answer)
4.8/5  (44)
(44)
Let be a vector in space with a, b > 0.
Compute the cross product and then use the result and the Lagrange Multiplier method to find the values of a and b such that the magnitude of the cross product is the largest with
(Essay)
4.8/5  (43)
(43)
Showing 21 - 40 of 77
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)