Exam 10: Approximating Functions Using Series
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
Estimate using a 4th degree Taylor Polynomial for about t = 1.Round to 4 decimal places.
(Short Answer)
4.7/5  (28)
(28)
A Taylor polynomial of degree six always has six non-zero terms.
(True/False)
4.8/5  (46)
(46)
Suppose that g is the pulse train of width 0.5.What percent of the energy of g is contained in the constant term of its Fourier series? Round to one decimal place.
(Short Answer)
4.8/5  (28)
(28)
The function is part of the normal probability density function (or bell-shaped curve).Find the Maclaurin series for by first finding the Maclaurin series for and then integrating it term by term.
(Multiple Choice)
4.7/5  (43)
(43)
According to the theory of relativity, the energy, E, of a body of mass m is given as a function of its speed, v, by , where c is a constant, the speed of light.Assuming v < c, expand E as a series in v/c, as far as the second non-zero term.If v = 0.05c, approximate E using your expansion.Also, approximate E by the formula .By what percentage do your two approximations differ?
(Short Answer)
4.8/5  (39)
(39)
What is the fourth degree Taylor polynomial for about x = 0?
(Multiple Choice)
4.8/5  (28)
(28)
The graph of y = f(x)is given below. 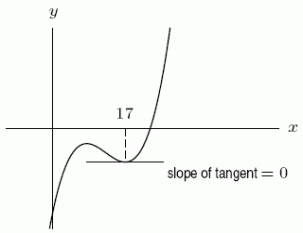 Suppose we approximate f(x)near x = 17 by the second degree Taylor polynomial centered about 17, .Is b positive, negative, or zero?
Suppose we approximate f(x)near x = 17 by the second degree Taylor polynomial centered about 17, .Is b positive, negative, or zero?
(Short Answer)
4.8/5  (33)
(33)
Find the third-degree Fourier polynomial for -2< 0< x\leq0 x\leq2 , where c is a constant, by writing a new function, , with period .
(Multiple Choice)
4.8/5  (39)
(39)
Approximate the function with a Taylor polynomial of degree 6.Use this to estimate the value of to 5 decimal places.
(Short Answer)
4.9/5  (40)
(40)
Suppose a function satisfies , , , and .What is the third degree Taylor polynomial for f about x = 5?
(Multiple Choice)
4.8/5  (30)
(30)
Suppose that you are told that the Taylor series of about x = 0 is .Find .
(Short Answer)
4.9/5  (39)
(39)
Estimate the magnitude of the error in approximating using a third degree Taylor polynomial about x = 0.
(Multiple Choice)
4.9/5  (41)
(41)
Use the Taylor polynomials for the sine and cosine functions to find a rational function with a degree 5 numerator and no fractional coefficients that approximates the tangent function near 0.
(Multiple Choice)
4.9/5  (40)
(40)
Use a Taylor polynomial of degree 3 for to approximate the value of .Give your answer to five decimal places.
(Multiple Choice)
4.7/5  (48)
(48)
Is a good bound for the maximum possible error for the nth degree Taylor polynomial about x = 0 approximating on the interval [0, 1]?
(True/False)
4.8/5  (34)
(34)
Recognize as a Taylor series evaluated at a particular value of x and find the sum to 4 decimal places.
(Short Answer)
4.7/5  (30)
(30)
Estimate using the first two terms of the Taylor series about x = -2 for .
(Multiple Choice)
4.7/5  (37)
(37)
Use the Taylor series for at x = 0 to find the Taylor series for at x = 0.
(Multiple Choice)
4.7/5  (37)
(37)
Showing 21 - 40 of 71
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)