Exam 8: Using the Definite Integral
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
A coffee filter is in the shape of a cone, as shown below.Suppose that when it is filled with water to a height h cm, the rate at which coffee flows out the hole at the bottom is given by Volume of coffee which flows out per second = cm3 / sec. 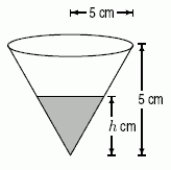 Approximately how many cubic centimeters are in the "slice" of coffee lying below h + h and above h?
Approximately how many cubic centimeters are in the "slice" of coffee lying below h + h and above h?
(Multiple Choice)
4.7/5  (37)
(37)
In a recent archaeological expedition, a scroll was discovered containing a description of a plan to build what appears to be the Tower of Babel.According to the manuscript, the tower was supposed to have a circular cross section and "go up to the heavens" (i.e., be infinitely high).A mathematician was consulted to solve some of the questions posed by the archaeologists.The mathematicians plotted half of the silhouette of the tower on a set of coordinate axes with the y-axis running through the center and discovered that it was approximated by the curve .The manuscript mentions that 2560 cubic "shrims" (Babel's unit of length)of stones were available to build the tower.The base of the tower was to have radius 3 shrims.Did they have enough?
(True/False)
4.9/5  (37)
(37)
Find the area inside the three-petal rose shown in the following figure.Round to 2 decimal places. 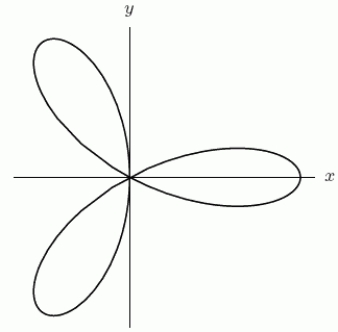
(Short Answer)
4.8/5  (35)
(35)
The density of cars (in cars per mile)down a 20-mile stretch of the Massachusetts Turnpike starting at a toll plaza is given by , where x is the distance in miles from the toll plaza and 0 x 20.Which of the following Riemann sums estimates the total number of cars down the 20-mile stretch?
(Multiple Choice)
4.8/5  (33)
(33)
Which of the following integrals determines the volume of a cone of height H and radius R?
(Multiple Choice)
4.8/5  (33)
(33)
When an oil well burns, sediment is carried up into the air by the flames and is eventually deposited on the ground.Less sediment is deposited further away from the oil well.Suppose that the density (in tons/square mile)at a distance r from the burning oil well is given by .Which Riemann sum approximates the total amount of sediment which is deposited within 100 miles of the well?
(Multiple Choice)
5.0/5  (33)
(33)
A plastic travel mug is made in two parts, the cup and the base.The cup part has outside shape and inside shape cut off at x = 4 as shown in the following figure. ![A plastic travel mug is made in two parts, the cup and the base.The cup part has outside shape y=\sqrt{x} and inside shape y=\sqrt[4]{x} cut off at x = 4 as shown in the following figure. If the cup is 14 cm tall, and the base is 10 cm in diameter and 1 cm thick, find the volume of plastic needed to make the mug.Round to 2 decimal places.](https://storage.examlex.com/TB4204/11eb1831_d910_7343_88c1_89ca61eb0e31_TB4204_00.jpg) If the cup is 14 cm tall, and the base is 10 cm in diameter and 1 cm thick, find the volume of plastic needed to make the mug.Round to 2 decimal places.
If the cup is 14 cm tall, and the base is 10 cm in diameter and 1 cm thick, find the volume of plastic needed to make the mug.Round to 2 decimal places.
(Short Answer)
4.9/5  (37)
(37)
A coffee filter is in the shape of a cone, as shown below.Suppose that when it is filled with water to a height h cm, the rate at which coffee flows out the hole at the bottom is given by
Volume of coffee which flows out per second = cm3 / sec. 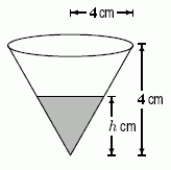 Suppose the coffee filter starts full.Write an integral representing the total amount of time it takes for the coffee filter to empty, and then evaluate it to find the time needed for the filter to empty.Give your answer to the nearest second.
Suppose the coffee filter starts full.Write an integral representing the total amount of time it takes for the coffee filter to empty, and then evaluate it to find the time needed for the filter to empty.Give your answer to the nearest second.
(Short Answer)
4.8/5  (27)
(27)
An insurance salesman offers you a life insurance policy with the following terms.You are to make payments at a rate of $1000 per year until age 70.If you pass away at any time, the policy will pay $150,000.Consider the payments to be made at a constant continuous rate of $1000 per year.You are 30 years old, and you have a bank account that you know will offer you 5% nominal annual interest compounded continuously for an indefinite amount of time.You could choose instead to make the $1000 payments into your bank account instead of paying for the insurance policy. If you stop these payments at age 70, just as you would stop making payments on the life insurance policy, then you would simply earn interest on the bank balance that you have accumulated to that point.If you feel that you are likely to live to be 76 years old, which is the better option?
(Multiple Choice)
4.7/5  (32)
(32)
The Great Cone of Haverford College is a monument built by freshmen during a customs week long, long ago.It is 100 ft.high and its base has a diameter of 100 ft.It has been built from bricks (purportedly made of straw)which weigh 2 lbs/ft3.Use a definite integral to approximate the number of foot-pounds required to build the Cone.Round to the nearest million. 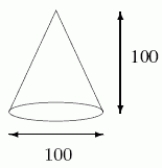
(Short Answer)
4.8/5  (26)
(26)
A large chocolate bar has trapezoidal cross section shown in the following figure.If you want the bar to have volume 861 cm3, what should H be? 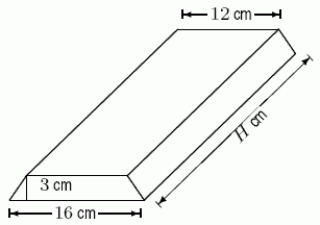
(Short Answer)
4.9/5  (43)
(43)
If it is known to take 147 joules of work to lift a box 1.5 meters off the floor, what is the mass of the box in kg?
(Short Answer)
4.8/5  (30)
(30)
In the following probability density function, is the mean smaller or greater than the median? 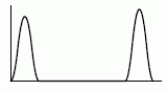
(Short Answer)
4.9/5  (30)
(30)
Consider the 3-sided region bounded by , and .The exact volume of the solid obtained when this region is rotated around the line x = -3 can be written as .Find Q.
(Short Answer)
4.8/5  (31)
(31)
You have $100,000 that you want to invest.Some "business men" are willing to sell you a machine for your $100,000 that prints money.You figure that every day you can print $200 with the machine, and you would deposit the $200 each day in a "special" bank account at BCCI.Your friends at BCCI will only be able to offer you 5% nominal annual interest, compounded continuously, due to the "sensitive nature" of the transaction.It would be your intention to print money each day for one year.Which of the following sums gives the value of your bank balance after one year?
(Multiple Choice)
4.9/5  (39)
(39)
Find the volume of the solid obtained by rotating the region bounded by , x = 0, y = 0, and y = -8 around y = 1.Round to 2 decimal places.
(Short Answer)
4.8/5  (37)
(37)
A swimming pool has shape as shown in the following figure. 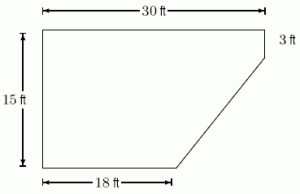 If the pool is 9 ft deep, how many foot-pounds does it take to pump all the water out? (Note: water weighs 62.4 pounds/ft3.)Round to the nearest whole number.
If the pool is 9 ft deep, how many foot-pounds does it take to pump all the water out? (Note: water weighs 62.4 pounds/ft3.)Round to the nearest whole number.
(Short Answer)
4.8/5  (34)
(34)
Focus on Engineering
It's time for the School of Engineering class picture and you are the photographer! You stand at the origin with your camera and your classmates are strung out along the curve from (0, 1)to . 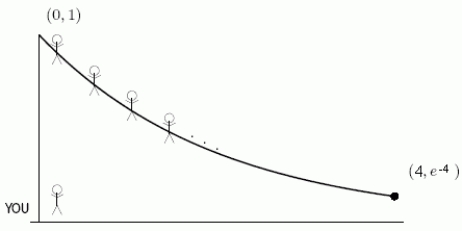 Use a calculator to find the average value of the distance from you to your classmates at a point (x, y)on the curve.Round to 3 decimal places.
Use a calculator to find the average value of the distance from you to your classmates at a point (x, y)on the curve.Round to 3 decimal places.
(Essay)
4.8/5  (34)
(34)
An object is in the shape drawn below; its boundary is obtained by rotating the parabola (for 0 x 1)around the y axis.(Units are in centimeters.)Suppose that the density of this object varies with height according to the rule (y)= 8 (2 - y)grams/cm3.Compute the mass in grams of this object.Give an exact answer and then round it to 2 decimal places. 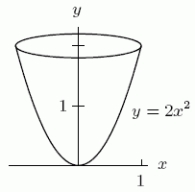
(Essay)
4.8/5  (31)
(31)
A cylindrically-shaped mug with a 3cm radius and a 10cm height is filled with tea.You have added some sugar to the tea, which tends to settle to the bottom of the mug.It turns out that the density of sugar (in gm/cm3)in the tea, as a function of the height, h, in cm, above the bottom of the mug, is given by the formula (h)= 0.025(10 - h).Which of the following Riemann sums approximates the total mass of sugar (in grams)in the mug of tea? 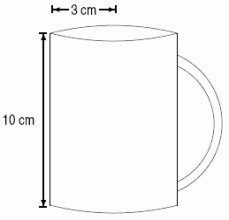
(Multiple Choice)
4.8/5  (36)
(36)
Showing 21 - 40 of 104
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)