Exam 8: Using the Definite Integral

It is estimated that in fifteen years, it will cost $200,000 to send a child to a four-year college.Suppose you want to set up an account at a bank that offers 8% nominal annual interest compounded continuously, so that 20 years from today, the account has $200,000 in it for your child's college education.Determine at what constant continuous rate K dollars per year you would need to deposit money as follows: Set up a differential equation for the rate of change of your bank balance, where B = f(t)is your bank balance at time t.Next, solve this differential equation for an initial balance of zero.Finally, use this result find K (to the nearest dollar).

A chlorine solution is poured over the surface of a rectangular swimming pool that is 20 meters long, 10 meters wide and 2 meters deep everywhere.Before the circulating pumps in the pool are turned on, it is discovered that the density of the chlorine solution at a height h meters above the bottom of the pool is given by $\rho$ (h)= 100h grams/m^3. In other words, the chlorine solution has distributed itself so that its density increases linearly from the bottom of the pool.Write a Riemann sum that approximates the total mass of chlorine solution in the pool, convert it into a definite integral, and evaluate it to find the total mass of the chlorine solution in the pool.Give your answer in kg.

The globular cluster M13 is a spherical distribution of stars which orbits our galaxy.Suppose that the density of stars in the cluster is purely a function of distance r from the center of the cluster and is given as $\rho(r)=\left(1+\left(\frac{r}{90}\right)^{3}\right)^{-5}$ stars/(ly)³, where r is measured in light-years, and 0 $\le$ r $\le$ 90 ly.(One light-year is the distance light travels in one year; "light-year" is abbreviated as "ly".)Find the number of stars in M13.Round to the nearest whole number.

You have a bank account that earns 8% nominal annual interest compounded continuously, and you want to have $90,000 in the bank account in five years so that you can buy a brand new Porsche.You decide to deposit money in the account at a constant continuous rate of K dollars per year.Use a Riemann sum followed by an integral to determine the value of K (to the nearest dollar)so that you will have the $90,000 after five years.

A study of the costs to produce airplanes in World War II led to the theory of "learning curves," the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x^th plane is given by $M C(x)=M M_{0} x^{\log _{2} 0.9}$ , where $M_{0}$ = marginal cost to produce the first plane.[Note: You may use the fact that $\log _{2} x=\frac{\ln x}{\ln 2}$ .] Recall that marginal cost is related to total cost as follows: $M C(x)=C^{\prime}(x)$ , where C(x)= total cost to produce x units. Given this, and the formula for MC(x)with $M_{0}$ = $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?

What is represented by the integral $\int_{0}^{6} \pi\left(36-h^{2}\right) d h$ ?

The circle $x^{2}+y^{2}=a^{2}$ is rotated around the y-axis to form a solid sphere of radius a.A plane perpendicular to the y-axis at y = a/5 cuts off a spherical cap from the sphere.What percent of the total volume of the sphere is contained in the cap? Round to 2 decimal places.

A study of the costs to produce airplanes in World War II led to the theory of "learning curves," the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x^th plane is given by $M C(x)=M M_{0} x^{\log _{2} 0.9}$ , where $M_{0}$ = marginal cost to produce the first plane.[Note: You may use the fact that $\log _{2} x=\frac{\ln x}{\ln 2}$ .] Recall that marginal cost is related to total cost as follows: $M C(x)=C^{\prime}(x)$ , where C(x)= total cost to produce x units. Given this, and the formula for MC(x)with $M_{0}$ = $500,000, find a formula for C(x).What, physically, is the meaning of the constant of integration in your formula?

The work done lifting a 5-lb bag of sugar 4 feet off the floor is _____ ft-lbs.

Circle City is circular with a radius of 3 miles.Right in the center is a circular park with radius one mile.No one lives in the park.Elsewhere the population density is 3000(5 - r)people per square mile, where r is the distance from the center in miles.What is the total population of Circle City, to the nearest thousand?

In a hydrogen atom in the unexcited state, the probability of finding the sole electron within x meters of the nucleus is given by $F(x)=\frac{4}{\left(a_{0}\right)^{3}} \int_{0}^{x} r^{2} e^{\frac{-2 r}{a_{0}}} d r$ , for $x \geq 0$ , where $a_{0}=5.29 \times 10^{-11}$ meters.What is the probability that the electron will be found within a sphere of radius $a_{0}$ ? Round to 3 decimal places.

A lightbulb company is interested in the lifespan of their lightbulbs.They have 20,000 lightbulbs burning and have collected the following information. After 2 months, 98% of the bulbs were still working. After 8 months, 80% of the bulbs were still working. We summarize all the data collected below: (Read carefully: the data was not collected at regular intervals.) How many bulbs out of the original 20,000 burned out during the first 4 months?

A professor gives the same 100-point final exam year after year and discovers that this students' scores tend to follow the triangular probability density function f(x)pictured below: 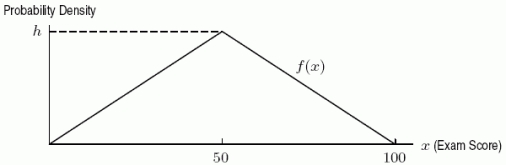Find the value of the height h of the triangular probability density function. (All persons, places, and events in this story are fictitious.Any similarity to real persons or situations is purely coincidental.)

Focus on Engineering It's time for the School of Engineering class picture and you are the photographer! You stand at the origin with your camera and your classmates are strung out along the curve $y=e^{-x}$ from (0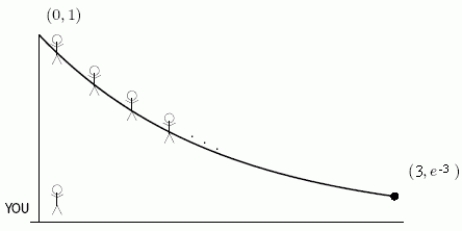, 1)to $\left(3, e^{-3}\right)$ . What is the formula for the average value of the distance from you to your classmates at points (x, y)on the curve?

A rectangular lake is 100 km long and 60 km wide.The depth of the water at any point of the surface is a tenth of the distance from the nearest shoreline.How many km³ of water does the lake contain? Round to the nearest whole number.

What is represented by the integral $\int_{0}^{4} \pi\left(\frac{x}{2}\right)^{2} d x$ ?

Suppose that the distribution of family sizes in the city of Boston in the year 1956 was given by: 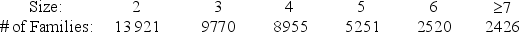If this data were represented on the following histogram as a density distribution function, what would be the height of the bar located at 3? Round to 2 decimal places.

Find the area outside the limaçon r = 1 + cos $\theta$ and inside the circle r = 2.Round to 2 decimal places.

In March 1995 the space shuttle carried an experiment designed by a Harvard student who studies the growth of crystals.Suppose the probability density function of the length, x cm, of a crystal grown in space is modeled by $p(x)=x e^{-x}$ for $x \geq 0$ .The cumulative distribution function giving the probability that a crystal has length $\le$ t cm is represented by P(t).Which of the quantities (i)- (x)below best approximates the probability that a crystal has length between 4 cm and 4.01 cm?

Suppose that the distribution of people's ages in the United States is essentially constant, or uniform, from age 0 to age 60, and from there it decreases linearly until age 100.This distribution p(x)is shown below, where x is age in years, and p measures probability density.Such a probability distribution is called trapezoidal. 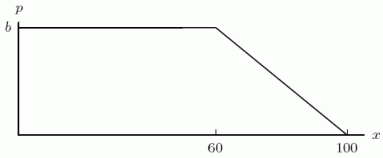Find the value of b.