Exam 2: Key Concept: the Derivative

Given the following data about a function f, estimate the rate of change of the derivative $f^{\prime}$ at x = 4.5. . x 3 3.5 4 4.5 5 5.5 6 f(x) 10 8 7 4 2 0 -1

If the Figure 1 is $f(x)$ , could Figure 2 be $f^{\prime \prime}(x)$ ? Figure 1 Figure 2

The cost of mining a ton of coal is rising faster every year.Suppose C(t)is the cost of mining a ton of coal at time t.Must C ''(t)be concave up?

The graph below shows the velocity of a bug traveling along a straight line on the classroom floor. 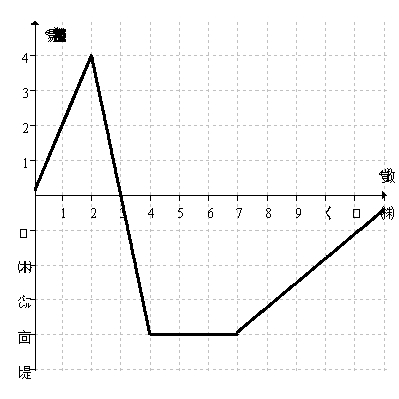When is the bug moving at a constant speed?

Estimate $\lim _{h \rightarrow 0} \frac{\sin \left(h^{2}\right)}{h}$ to 2 decimal places by substituting smaller and smaller values of h (use radians).

A function that has an instantaneous rate of change of 3 at a point (x, y)can fail to be continuous at that point.

Sketch a graph of a continuous function f(x)with the following properties: • f'(x)< 0 for x < 4 • f'(x)> 0 for x > 4 • f'(4)is undefined

Let $f(x)=x^{\sin x}$ .Using your calculator, estimate f '(7)to 3 decimal places.

Use the limit of the difference quotient to find the derivative of $g(x)=\frac{11}{x+1}$ at the point (1, 11/2).

Could the first graph, A be the derivative of the second graph, B? 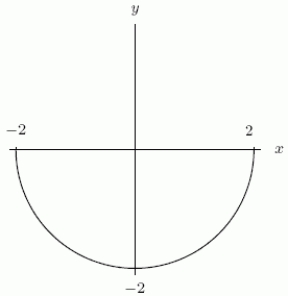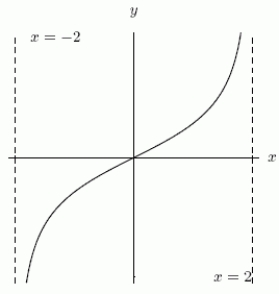A B

Every day the Office of Undergraduate Admissions receives inquiries from eager high school students.They keep a running account of the number of inquiries received each day, along with the total number received until that point.Below is a table of weekly figures from about the end of August to about the end of October of a recent year. Week di Inquiries That Week Total for Yeal 8/28-9/01 1085 11,928 9/04-9/08 1193 13,121 9/11-9/15 1312 14,433 9/18-9/22 1443 15,876 9/25-9/29 1588 17,464 10/02-10/06 1746 19,210 10/09-10/13 1921 21,131 10/16-10/20 2113 23,244 10/23-10/27 2325 25,569 Based on the table determine a formula that approximates the total number of inquiries received by a given week.Use your formula to estimate how many inquiries the admissions office will have received by November 24.

Alone in your dim, unheated room you light one candle rather than curse the darkness.Disgusted by the mess, you walk directly away from the candle.The temperature (in ${ } ^ { \circ } F$ )and illumination (in % of one candle power)decrease as your distance (in feet)from the candle increases.The table below shows this information. distance(feet) Temp. () illuminatiou (\%) 0 55 100 1 54.5 85 2 53.5 75 3 52 67 4 50 60 5 47 56 6 43.5 53 You are cold when the temperature is below 40°F.You are in the dark when the illumination is at most 50% of one candle power.Suppose you know that at 6 feet the instantaneous rate of change of the temperature is -4.5° F/ft and the instantaneous rate of change of illumination is -3% candle power/ft.Are you in the dark before you are cold, or cold before you are dark?

Let L(r)be the amount of board-feet of lumber produced from a tree of radius r (measured in inches).What does L(16)mean in practical terms?

Let S(t)represent the number of students enrolled in school in the year t.If the number of students enrolling is increasing faster and faster, then is S '(t)positive, negative, or 0?

Describe two ways that a continuous function can fail to have a derivative at a point, x = a.Illustrate your description with graphs.

Given the following data about a function f(x), the equation of the tangent line at x = 5 is approximated by x 3 3.5 4 4.5 5 5.5 6 f(x) 10 8 7 4 2 0 -1

Alone in your dim, unheated room you light one candle rather than curse the darkness.Disgusted by the mess, you walk directly away from the candle.The temperature (in ${ } ^ { \circ } F$ )and illumination (in % of one candle power)decrease as your distance (in feet)from the candle increases.The table below shows this information. distance(feet) Temp. () illuminatiou (\%) 0 55 100 1 54.5 85 2 53.5 75 3 52 67 4 50 60 5 47 56 6 43.5 53 Suppose you know that at 6 feet the instantaneous rate of change of the illumination is -3.5 % candle power/ft.At 7 feet, the illumination is approximately _____ % candle power.

Use the graph of $5.5 e^{3 x}$ at the point (0, 5.5)to estimate $f^{\prime}(0)$ to three decimal places.

A function defined for all x has the following properties: • f is increasing • f is concave down • f (3)= 2 • f '(3)= 1/2 How many zeros does f(x)have in the interval $1 \leq x \leq 3$ ?

A husband and wife purchase life insurance policies.Over the next 40 years, one policy pays out when the husband dies, and the other pays out when both husband and wife die.Their life expectancy is 20 years, and the probability that both die before year t is given by the function $f_{T}(t)=\frac{1}{1600} t^{2}$ .How fast is the probability that both are dead increasing in 25 years?