Exam 13: Multiple Regression Analysis
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
In multiple regression analysis involving 10 independent variables and 100 observations, the critical value of t for testing individual coefficients in the model will have:
(Multiple Choice)
4.9/5  (33)
(33)
Three qualitative variables need to be incorporated into a regression model. The first variable has 5 possible categories, the second one has 3 possible categories, and the third one has 2 possible categories. Based on this information, ten dummy variables need to be included in the regression model.
(True/False)
4.8/5  (33)
(33)
A multiple regression model has the form: 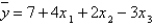 . As
. As 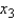 increases by 1 unit, with
increases by 1 unit, with 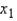 and
and 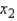 held constant, then y on average is expected to:
held constant, then y on average is expected to:
(Multiple Choice)
4.7/5  (39)
(39)
If a multiple regression model includes 10 or more predictor variables, it is almost certain that changes in the predictor variables cause changes in the response variable y.
(True/False)
4.7/5  (37)
(37)
Three predictor variables are being considered for use in a linear regression model. 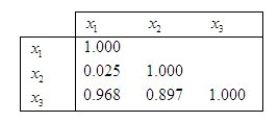 Given the correlation matrix above, does it appear that multicollinearity could be a problem?
______________
Explain.
________________________________________________________
Given the correlation matrix above, does it appear that multicollinearity could be a problem?
______________
Explain.
________________________________________________________
(Essay)
4.8/5  (40)
(40)
Assume that a company is tracking their advertising expenditures as they relate to television ( 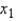 ) and radio advertising (
) and radio advertising ( 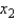 ). The owner of the company believes that it would improve the regression model to add a third variable that represents the sum of the advertising on radio and television (
). The owner of the company believes that it would improve the regression model to add a third variable that represents the sum of the advertising on radio and television ( 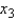 =
= 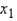 +
+ 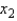 ). This assessment is generally correct.
). This assessment is generally correct.
(True/False)
4.8/5  (29)
(29)
The sequential sums of squares represent the conditional contribution of each of the predictor variables given the variables already in the model. Use the following partial output generated using Minitab to determine which predictor variable accounts for the largest proportion of the total variation explained by the regression model. 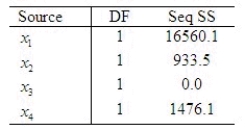 Which variable accounts for the largest proportion?
______________
What is the proportion accounted by the selected variable?
______________ Enter a decimal percent or use the % sign.
Which variable accounts for the largest proportion?
______________
What is the proportion accounted by the selected variable?
______________ Enter a decimal percent or use the % sign.
(Short Answer)
4.9/5  (34)
(34)
A multiple regression model has the form 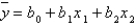 . The coefficient
. The coefficient 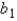 is interpreted as the:
is interpreted as the:
(Multiple Choice)
4.9/5  (29)
(29)
A multiple regression analysis includes 25 data points and 4 independent variables produces SST = 400 and SSR = 300. Then, the multiple standard error of estimate is 5.
(True/False)
4.9/5  (37)
(37)
The multiple coefficient of determination measures the proportion or percentage of variation in the dependent variable that is explained by the independent variables included in the model.
(True/False)
4.8/5  (30)
(30)
In a multiple regression model, if the residuals have a constant variance, which of the following should be evident?
(Multiple Choice)
4.7/5  (43)
(43)
The first-order model 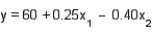 attempts to explain average air temperatures in degrees Fahrenheit for a particular day as a function of distance from the coast (
attempts to explain average air temperatures in degrees Fahrenheit for a particular day as a function of distance from the coast ( 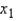 in miles), and altitude (
in miles), and altitude ( 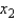 in hundreds of feet). Interpret the parameters
in hundreds of feet). Interpret the parameters 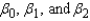 .
. 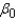 = ______________
Interpret
= ______________
Interpret 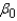 .
______________
.
______________ 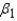 = ______________
Interpret
= ______________
Interpret 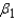 .
______________
.
______________ 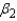 = ______________
Interpret
= ______________
Interpret 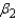 .
______________
.
______________
(Essay)
4.8/5  (38)
(38)
Suppose that you fit the model 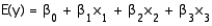 to 15 data points and found F equal to 52.36.
Do the data provide sufficient evidence to indicate that the model contributes information for the prediction of y? Test using a 5% level of significance.
______________
Use the value of F to calculate
to 15 data points and found F equal to 52.36.
Do the data provide sufficient evidence to indicate that the model contributes information for the prediction of y? Test using a 5% level of significance.
______________
Use the value of F to calculate 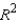 .
______________
Interpret its value.
________________________________________________________
.
______________
Interpret its value.
________________________________________________________
(Essay)
5.0/5  (39)
(39)
For a multiple regression model the following statistics are given: Total SS = 400, SSR = 350, k = 4, and n = 20. The coefficient of determination adjusted for degrees of freedom is:
(Multiple Choice)
4.9/5  (25)
(25)
In order to test the validity of a multiple regression model involving 5 independent variables and 30 observations, the numerator and denominator degrees of freedom for the critical value of F are, respectively,
(Multiple Choice)
4.9/5  (45)
(45)
Multicollinearity is a situation in which two or more of the independent variables are highly correlated with each other.
(True/False)
4.9/5  (37)
(37)
In a multiple regression analysis involving 4 predictor variables, and 25 observations, the total sum of squares is 800, and the error sum of squares is 200. The value of the F-test statistic for testing the usefulness of this model must be:
(Multiple Choice)
4.9/5  (32)
(32)
Stepwise regression analysis is most useful when it is anticipated that there are curvilinear relationships between the dependent variable and the potential independent variables.
(True/False)
4.8/5  (38)
(38)
Showing 101 - 120 of 178
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)