Exam 6: The Normal Probability Distribution

Suppose the current median age of U.S. citizens is 30. If a survey of 500 randomly selected U.S. citizens is conducted, what is the probability at most 240 of them will be under 30 years old? ______________

In general, the binomial probability P(X = x) is approximated by the area under a normal curve between x - .5 and x + .5.

Historical data collected at First of America Bank in Michigan revealed that 80% of all customers applying for a loan are accepted. Suppose that 50 new loan applications are selected at random. Find the expected value of the number of loans that will be accepted by the bank. ______________ Find the standard deviation of the number of loans that will be accepted by the bank. ______________ What is the probability that at least 42 loans will be accepted? ______________ What is the probability that the number of loans rejected is between 10 and 15, inclusive? ______________

Using the standard normal curve, the area between z = 0 and z = 3.50 is about 0.50.

A standard normal distribution is a normal distribution with:

Let 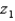be a z-score that is unknown but identifiable by position and area. If the area to the right of 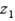is 0.8413, the value of 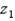is 1.0.

Let 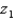be a z-score that is unknown but identifiable by position and area. If the symmetrical area between - 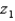and + 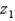is 0.903, the value of 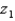is 1.66.

For a normal curve, if the mean is 25 minutes and the standard deviation is 5 minutes, the area to the left of 10 minutes is about 0.50.

Which of the following distributions are always symmetrical?

The normal probability distribution is important because a large number of random variables observed in nature possess a frequency distribution that is approximately a normal probability distribution.

The z-score representing the 10th percentile of the standard normal curve is -1.28.

Which of the following correctly describes a continuous random variable?

Do Americans tend to vote for the taller of the two candidates in a presidential election? In 30 of our presidential elections since 1856, 18 of the winners were taller than their opponents. Assume that Americans are not biased by a candidate's height and that the winner is just as likely to be taller or shorter than his opponent. Is the observed number of taller winners in the U.S. presidential elections unusual? Find the approximate probability of finding 18 or more of the 30 pairs in which the taller candidate wins. ______________ Based on your answer to part (a), can you conclude that Americans consider a candidate's height when casting their ballot? ______________

Given that Z is a standard normal random variable, what is the value z if the area to the right of z is 0.9066?

If z is a standard normal random variable, the area between z = 0.0 and z = 1.20 is 0.3849, while the area between z = 0.0 and z = 1.40 is 0.4192. What is the area between z = -1.20 and z = 1.40?

Suppose the amount of tar in cigarettes is normally distributed with mean 3.5 mg and standard deviation 0.5 mg. What proportion of cigarettes have a tar content exceeding 4.25 mg? ______________ "Low tar" cigarettes must have tar content below the 25th percentile of the tar content distribution. What is the value, which is the 25th percentile of the tar content distribution? ______________

The time necessary to assemble a discount store display is normally distributed with 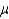= 5 minutes and 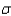= 30 seconds. A large number of potential employees are timed assembling a practice display. How much time (in minutes) should the personnel manager allow the potential employees to assemble the display if the store wants only 80% of the people to complete the task? ______________ minutes

If Z is a standard normal random variable, the area between z = 0.0 and z = 1.30 is 0.4032, while the area between z = 0.0 and z = 1.50 is 0.4332. What is the area between z = -1.30 and z = 1.50?

The weights of cans of soup produced by a company are normally distributed with a mean of 15 ounces and a standard deviation of 0.5 ounces. What is the probability that a can of soup selected randomly from the entire production will weigh at most 14.3 ounces? ______________ Determine the minimum weight of the heaviest 5% of all cans of soup produced. ______________ If 28,390 of the cans of soup of the entire production weigh at least 15.75 ounces, how many cans of soup have been produced? ______________

The normal approximation to the binomial distribution works best when the number of trials is large, and when the binomial distribution is symmetrical (like the normal).