Exam 6: The Normal Probability Distribution
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
If x is a normal random variable with mean of 2 and standard deviation of 5, then P(x < 3) = P(x > 7).
(True/False)
4.9/5  (34)
(34)
The owner of a fish market determined that the average weight for a catfish is 3.6 pounds with a standard deviation of 0.8 pound. Assume the weights of catfish are normally distributed.
What is the probability that a randomly selected catfish will weigh more than 4.8 pounds?
______________
What is the probability that a randomly selected catfish will weigh between 3 and 5 pounds?
______________
A randomly selected catfish will weigh more than x pounds to be one of the top 5% in weight. What is the value of x?
______________
A randomly selected catfish will weigh less than x pounds to be one of the bottom 20% in weight. What is the value of x?
______________
Above what weight (in pounds) do 87.70% of the weights occur?
______________
What is the probability that a randomly selected catfish will weigh less than 3.2 pounds?
______________
Below what weight (in pounds) do 83.4% of the weights occur?
______________
(Short Answer)
4.8/5  (41)
(41)
The average length of time required to complete a college achievement test was found to equal 75 minutes, with a standard deviation of 15 minutes. When should the test be terminated if you wish to allow sufficient time for 90% of the students to complete the test? (Assume that the time required to complete the test is normally distributed.)
______________
(Short Answer)
5.0/5  (38)
(38)
Given that Z is a standard normal random variable, P(Z > -1.58) is:
(Multiple Choice)
4.7/5  (38)
(38)
If x is normally distributed random variable with a mean of 8.20 and variance of 4.41, and that P(x > b) = .08, then the value of b is:
(Multiple Choice)
4.8/5  (41)
(41)
Given a normal random variable x with mean 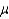 and standard deviation
and standard deviation 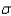 , the mean of the standard normal random variable z associated with x is 1.
, the mean of the standard normal random variable z associated with x is 1.
(True/False)
4.9/5  (38)
(38)
For some positive value of z, the probability that a standard normal variable is between 0 and z is 0.3770. The value of z is:
(Multiple Choice)
4.7/5  (42)
(42)
Assume that x is normally distributed random variable with a mean of 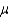 and a standard deviation of .15. Given this information and that P(x < 2.10) = .025, what is the value of
and a standard deviation of .15. Given this information and that P(x < 2.10) = .025, what is the value of 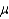 ?
?
(Multiple Choice)
4.8/5  (38)
(38)
Given that X is a binomial random variable, the binomial probability P(X 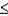 x) is approximated by the area under a normal curve to the left of:
x) is approximated by the area under a normal curve to the left of:
(Multiple Choice)
4.8/5  (34)
(34)
The probability density function f(x) of a random variable X that is normally distributed is completely determined once the:
(Multiple Choice)
4.8/5  (29)
(29)
Assume that x is a normally distributed random variable with a mean equal to 13.4 and a standard deviation equal to 3.6. Given this information and that P(x > a) = .05, the value of a must be 19.322.
(True/False)
4.8/5  (41)
(41)
The gestation time for human babies is approximately normally distributed with an average of 280 days and a standard deviation of 12.
Find the upper quartile for the gestation times.
______________
Find the lower quartile for the gestation times.
______________
Would it be unusual to deliver a baby after only 6 months of gestation?
______________
Explain.
________________________________________________________
(Essay)
4.7/5  (35)
(35)
Which of the following is not true for a normal distribution?
(Multiple Choice)
4.9/5  (33)
(33)
For a car traveling 35 miles per hour (mph), the distance required to brake to a stop is normally distributed with mean of 55 feet and a standard deviation of 8 feet. Suppose you are traveling 35 mph in a residential area and a car moves abruptly into your path at a distance of 65 feet.
If you apply your brakes, what is the probability that you will brake to a stop within 45 feet or less?
______________
Within 55 feet or less?
______________
If the only way to avoid a collision is to brake to a stop, what is the probability that you will avoid the collision?
______________
(Short Answer)
4.9/5  (34)
(34)
Let x be a binomial random variable with n = 25 and p = 0.3.
Is the normal approximation appropriate for this binomial random variable?
______________
Find the mean for x.
______________
Find the standard deviation for x.
______________
Use the normal approximation to find 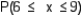 .
______________
Use the cumulative binomial probabilities table in Appendix 1 of your book to calculate the exact probability, above.
______________
Compare the results of the last two questions. Was your approximation close, or far, from the exact answer?
______________
.
______________
Use the cumulative binomial probabilities table in Appendix 1 of your book to calculate the exact probability, above.
______________
Compare the results of the last two questions. Was your approximation close, or far, from the exact answer?
______________
(Short Answer)
4.8/5  (26)
(26)
The scores on a national achievement test were normally distributed, with a mean of 550 and a standard deviation of 112.
If you achieved a score of 690, how far, in standard deviations, did your score depart from the mean?
______________
What percentage of those who took the examination scored higher than you?
______________
(Short Answer)
4.9/5  (39)
(39)
Let x denote a normal random variable with mean 30 and standard deviation 5. What x-value is the 67th percentile of this distribution?
______________
(Short Answer)
4.9/5  (30)
(30)
A normal random variable x has mean 54 and standard deviation 15.
Would it be unusual to observe the value x = 0?
______________
Explain.
________________________________________________________
(Essay)
4.7/5  (38)
(38)
A normal random variable x has mean 36.7 and standard deviation 10. Find a value of x that has area 0.01 to its right.
______________
(Short Answer)
4.7/5  (42)
(42)
Let 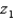 be a z score that is unknown but identifiable by position and area. If the symmetrical area between a negative
be a z score that is unknown but identifiable by position and area. If the symmetrical area between a negative 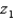 and a positive
and a positive 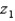 is 0.8132, then the value of
is 0.8132, then the value of 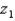 is:
is:
(Multiple Choice)
4.7/5  (42)
(42)
Showing 81 - 100 of 196
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)