Exam 6: The Normal Probability Distribution
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
Suppose the numbers of a particular type of bacteria in samples of 1 milliliter (ml) of drinking water tend to be approximately normally distributed, with a mean of 80 and a standard deviation of 10.
What is the probability that a given 1-ml sample will contain more than 100 bacteria?
______________
(Short Answer)
4.8/5  (37)
(37)
The time it takes Jessica to bicycle to school is normally distributed with mean 15 minutes and variance 4. Jessica has to be at school at 8:00 am. Suppose you saw her at class, and she said it took her 23 minutes to get to school that day. Which of the following is a reasonable inference or conclusion?
(Multiple Choice)
4.9/5  (33)
(33)
Given a normal random variable x with mean 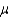 and standard deviation
and standard deviation 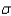 , the standard normal random variable associated with x is
, the standard normal random variable associated with x is 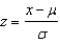 .
.
(True/False)
4.8/5  (37)
(37)
Using the standard normal curve, the area between z = 0 and z = 2.2 is 0.4868.
(True/False)
4.9/5  (42)
(42)
Two students are enrolled in an introductory statistics class at the university. The first student is in a morning section and the second student is in an afternoon section. Assume test scores are normally distributed. In the morning section, the mean was 64 and the standard deviation was 8. In the afternoon section, the class mean was 60 with a standard deviation of 7.5. If the student in the morning section takes a midterm exam and earns a score of 76, while the student in the afternoon section takes a midterm exam and earns a score of 72, which student performed better compared to the rest of the students in his or her respective class?
______________
Explain.
________________________________________________________
(Essay)
5.0/5  (34)
(34)
For some positive value of x, the probability that a standard normal variable is between 0 and + 1.5x is 0.4332. The value of x is:
(Multiple Choice)
4.9/5  (36)
(36)
Given a normal random variable x with mean of 82 and standard deviation of 12, the value of the standard normal random variable z associated with x = 70 is smaller than zero.
(True/False)
4.9/5  (34)
(34)
For some value of z, the probability that a standard normal variable is below z is 0.2090. The value of z is:
(Multiple Choice)
4.8/5  (37)
(37)
Given a normal random variable x with mean of 70 and standard deviation of 12, the value of the standard normal random variable z associated with x = 82 is larger than zero.
(True/False)
4.8/5  (37)
(37)
The distribution of IQ scores for high school graduates is normally distributed with 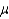 = 104 and
= 104 and 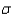 = 16.
Find the probability a person chosen at random from this group has an IQ score above 146.08.
______________
What fraction of the IQ scores would be between 97 and 126?
______________
What is the 95th percentile of this normal distribution?
______________
= 16.
Find the probability a person chosen at random from this group has an IQ score above 146.08.
______________
What fraction of the IQ scores would be between 97 and 126?
______________
What is the 95th percentile of this normal distribution?
______________
(Short Answer)
4.8/5  (35)
(35)
The time it takes a student to finish a final exam test is known to be normally distributed with a mean equal to 84 minutes with a standard deviation equal to 10 minutes. Given this information, the probability that it will take a randomly selected student between 75 and 90 minutes is approximately .0902.
(True/False)
4.9/5  (35)
(35)
The scores on an aptitude test are normally distributed with an unknown mean, a variance of 36, and only 7% of the scores below 26.
What is the mean score?
______________
(Short Answer)
4.8/5  (44)
(44)
The normal probability distribution is one of the most commonly used discrete probability distributions.
(True/False)
4.9/5  (36)
(36)
If Z is a standard normal random variable, then P(-1.75 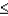 Z
Z 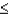 -1.25) is:
-1.25) is:
(Multiple Choice)
4.9/5  (35)
(35)
Using the standard normal curve, the z-score representing the 75th percentile is 0.67.
(True/False)
4.9/5  (38)
(38)
How does the IRS decide on the percentage of income tax returns to audit for each state? Suppose they do it by randomly selecting 50 values from a normal distribution with a mean equal to 1.25% and a standard deviation equal to 0.4%.
What is the probability that a particular state will have more than 2% of its income tax returns audited?
______________
What is the probability that a state will have less than 1% of its income tax returns audited?
______________
(Short Answer)
4.8/5  (48)
(48)
A recent survey of university faculty reported 55% were considering going into another profession. Based on this information, what is the expected number of faculty who would be considering going into another profession if we randomly sampled 200 faculty members?
______________
What is the approximate probability 60 or more faculty from a random sample of 200 would be considering going into another profession?
______________
(Short Answer)
4.7/5  (39)
(39)
Given that X is a binomial random variable, the binomial probability P(X  x) is approximated by the area under a normal curve to the right of:
x) is approximated by the area under a normal curve to the right of:
(Multiple Choice)
4.8/5  (39)
(39)
A standard normal curve is a normal probability density function with a mean of 1 and a standard deviation of 0.
(True/False)
4.8/5  (34)
(34)
Showing 61 - 80 of 196
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)