Exam 6: The Normal Probability Distribution
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
Given that Z is a standard normal variable, the value z for which P(Z 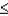 z) = 0.2580 is:
z) = 0.2580 is:
(Multiple Choice)
5.0/5  (36)
(36)
A student government representative claims that 55% of the student body of a local university favor a move to Division I in college football. A random sample of 2000 students is selected.
What is the expected number of students that will favor the move to Division I?
______________
What is the approximate probability that less than 1150 students of the 2000 selected will favor the move to Division I?
______________
(Short Answer)
4.8/5  (41)
(41)
Given that Z is a standard normal random variable, P(-1.0 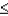 Z
Z 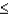 1.5) is:
1.5) is:
(Multiple Choice)
4.8/5  (37)
(37)
In general, the binomial probability P(X  x) is approximated by the area under the normal curve to the right of x - .5.
x) is approximated by the area under the normal curve to the right of x - .5.
(True/False)
4.9/5  (37)
(37)
Many different types of continuous random variables give rise to a large variety of probability density functions, including:
(Multiple Choice)
4.9/5  (34)
(34)
Given a normal random variable x with mean 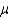 and standard deviation
and standard deviation 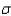 , the variance of the standard normal random variable z associated with x is 0.
, the variance of the standard normal random variable z associated with x is 0.
(True/False)
4.9/5  (37)
(37)
A car dealership has found that the length of time before a major repair is required on the new cars it sells is normally distributed, with a mean equal of 36 months and a standard deviation of 9 months. If the dealer wants only 5% of the cars to fail before the end of the guarantee period, for how many months should the cars be guaranteed?
______________
(Short Answer)
4.8/5  (42)
(42)
Using the standard normal curve, the area between z = -1.50 and z = 1.50 is 0.4332.
(True/False)
4.7/5  (39)
(39)
The z-score representing the first quartile of the standard normal distribution is:
(Multiple Choice)
4.8/5  (41)
(41)
A random variable x is normally distributed with m = 100 and 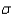 = 20.
What is the median of this distribution?
______________
Find
= 20.
What is the median of this distribution?
______________
Find 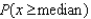 .
______________
Find
.
______________
Find 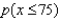 .
______________
.
______________
(Short Answer)
4.9/5  (43)
(43)
Given that Z is a standard normal random variable, the area to the left of a value z is expressed as:
(Multiple Choice)
4.9/5  (49)
(49)
The normal random variable's density function is (1) single-peaked above the variable's mean, median, and mode, all of which are equal to one another, (2) perfectly symmetric about this peaked central value and, thus, bell-shaped, and (3) characterized by tails extending indefinitely in both directions from the center, approaching (but never touching) the horizontal axis, which implies a positive probability for finding values of the random variable anywhere between minus infinity and plus infinity.
(True/False)
4.8/5  (37)
(37)
Let 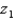 be a z-score that is unknown but identifiable by position and area. If the symmetrical area between -
be a z-score that is unknown but identifiable by position and area. If the symmetrical area between - 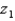 and +
and + 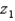 is 0.9544, the value of
is 0.9544, the value of 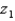 is 2.0.
is 2.0.
(True/False)
4.8/5  (37)
(37)
One difference between a binomial random variable x and a standard normal random variable z is that with the binomial random variable we cannot determine P(x = a), while for the standard normal variable we can determine P(z = a).
(True/False)
4.9/5  (44)
(44)
Which of the following is not a characteristic of the normal distribution?
(Multiple Choice)
4.9/5  (35)
(35)
For a continuous random variable, P(x  a) = P(x > a) because P(x = a) = 0.
a) = P(x > a) because P(x = a) = 0.
(True/False)
4.8/5  (36)
(36)
If x is a normal random variable with mean 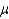 = 4 and standard deviation
= 4 and standard deviation 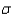 = 2, and Y is a normal random variable with mean
= 2, and Y is a normal random variable with mean 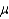 = 10 and standard deviation
= 10 and standard deviation 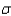 = 5, then P(x < 0) = P(Y < 0).
= 5, then P(x < 0) = P(Y < 0).
(True/False)
4.9/5  (42)
(42)
A chemical manufacturer sells its product in steel drums. The net weight of the chemical in the drums has a normal distribution with mean 310 pounds and standard deviation 4 pounds. The manufacturer guarantees its customers each drum will contain at least 300 pounds of the chemical.
What percentage of the drums will satisfy this guarantee?
______________
(Short Answer)
4.8/5  (32)
(32)
Using the standard normal curve, the z-score representing the 90th percentile is 1.28.
(True/False)
4.9/5  (41)
(41)
Twenty-five psychology instructors have formed a committee to pick next year's textbook, and they have narrowed their decision down to two equally good books, one with a better bibliography and references, and the other with a better format and illustrations. Since the books are considered to be equally good, we will assume the probability an instructor chooses either book is 0.5 and the instructors' decisions are made independently.
Using the binomial distribution, find the probability 15 or more instructors choose the book with the better format and illustrations.
______________
Use the normal approximation to the binomial to find the probability 15 or more instructors choose the book with the better format and illustrations.
______________
Compare the results in parts (a) and (b). Is the normal approximation a good approximation?
______________
(Short Answer)
4.8/5  (40)
(40)
Showing 121 - 140 of 196
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)