Exam 2: Describing Data With Numerical Measures

You are given the data values 5, 10, 15, 20, and 25. If these data were considered to be a population, and you calculated the mean, you would get the same answer as if these data were considered to be a sample from another larger population.

The mode of a data set or a distribution of measurements, if it exists, is unique.

From a sample of size 100, the following descriptive measures were calculated: median = 23, mean = 20, standard deviation = 5, range = 35; seventy-five sample values are between 10 and 30; and ninety-nine sample values are between 5 and 35. If you knew the sample mean, median, and standard deviation were correct, which one of the following conclusions might you draw?

Any unusually large observation (as measured by a z-score greater than 3), or any unusually small observation (as measured by a z-score smaller than -3) is considered an outlier.

Tchebysheff's Theorem states that the percentage of measurements in a data set that fall within three standard deviations of their mean is:

Incomes of workers in an automobile company in Michigan are known to be right - skewed with a mean equal to $36,100. If at least 8/9 of all incomes are in the range of $29,600 to $42,800, and this was based on Tchebysheff's Theorem, what is the standard deviation for the auto workers?

Twenty-eight applicants interested in working for the Food Stamp program took an examination designed to measure their aptitude for social work. A stem-and-leaf plot of the 28 scores appears below, where the first column is the count per branch, the second column is the stem value, and the remaining digits are the leaves. 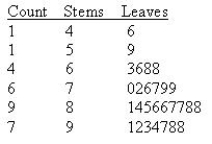What is the value of the first quartile? Q1 = ______________ What is the value of the third quartile? Q3 = ______________ What is the interquartile range? IQR = ______________ Find the inner fences. ______________ Find the outer fences. ______________ Construct a boxplot for this data. Does the boxplot indicate the presence of any outliers? ______________

Which of the following statements is true for the following data values: 17, 15, 16, 14, 17, 18, and 22?

Given a distribution of measurements that is approximately mound-shaped, the Empirical Rule states that the approximate percentage of measurements in a data set that fall within two standard deviations of their mean is approximately:

Twenty-eight applicants interested in working for the Food Stamp program took an examination designed to measure their aptitude for social work. A stem-and-leaf plot of the 28 scores appears below, where the first column is the count per "branch," the second column is the stem value, and the remaining digits are the leaves. 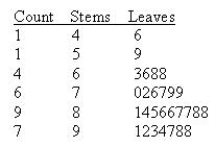a. Should the Empirical Rule be applied to this data set? ______________ b. Use the range approximation to determine an approximate value for the standard deviation. ______________ Is this a good approximation? ______________

The expression , where is recognizable as the formula for:

Consider the following set of measurements: 5.4, 5.9, 3.5, 4.1, 4.6, 2.5, 4.7, 6.0, 5.4, 4.6, 4.9, 4.6, 4.1, 3.4, 2.2 You may use the Data Analysis tool if you want. a. Find the 25^th percentile: ______________, Find the 50^th percentile: ______________, Find the 75^th percentile: ______________. b. What is the value of the interquartile range? ______________

A distribution is said to be skewed to the right if the population mean is larger than the sample mean.

The value of the mean times the number of observations equals the sum of all of the observations.

The standard deviation is expressed in terms of the original units of measurement but the variance is not.

The interquartile range is the difference between the lower and upper quartiles.

The following five-number summary for a sample of size 500 were obtained: Minimum = 250, 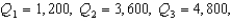and Maximum = 4,950. Based on this information, if you were to construct a box and whisker plot, the value corresponding to the right - hand edge of the box would be 4,800.

The sum of the deviations squared from the mean is always zero.

The distribution of credit card balances for customers is highly skewed to the right with a mean of $1,200 and a standard deviation of $150. Based on this information, approximately 68% of the customers will have credit card balances between $1,050 and $1,350.

A data sample has a mean of 87, and a median of 117. The distribution of the data is positively skewed.