Exam 12: Vector-Valued Functions
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Find a vector-valued function, using the given parameter, to represent the intersection of the surfaces given below. Surfaces Parameter z=+,y+8x=0 x=t
(Multiple Choice)
4.7/5  (31)
(31)
Find the curvature K of the curve Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (27)
(27)
Find a vector-valued function, using the given parameter, to represent the intersection of the surfaces given below. Surfaces Parameter +=25,z= x=52\pit
(Multiple Choice)
4.8/5  (39)
(39)
A baseball is hit 5 feet above the ground at 95 feet per second and at an angle of with respect to the ground. Find the arc length of the trajectory. Round your answer to one decimal place.
(Multiple Choice)
4.8/5  (42)
(42)
Use the properties of the derivative to find vector-valued functions. (t)=2t-3+3 (t)=3+5+4
(Multiple Choice)
4.9/5  (44)
(44)
A 5700-pound vehicle is driven at a speed of 25 miles per hour on a circular interchange of radius 90 feet. To keep the vehicle from skidding off course, what frictional force must The road surface exert on the tires? Round your answer to one decimal place.
(Multiple Choice)
4.8/5  (36)
(36)
Determine the interval on which the vector-valued function is continuous.
(Multiple Choice)
4.8/5  (37)
(37)
Find the domain of the vector-valued function given below. where
(t)=++(t-4) (t)=+t+(t-1)
(Multiple Choice)
4.9/5  (32)
(32)
Determine the maximum height of a projectile fired at a height of 6 feet above the ground with an initial velocity of 700 feet per second and at an angle of Use the model for projectile motion, assuming there is no air resistance. Round your answer to three
Decimal places.
(Multiple Choice)
4.8/5  (48)
(48)
Use the given acceleration function and initial conditions to find the position at time t ,
(Multiple Choice)
4.8/5  (38)
(38)
The graph below is most likely the graph of which of the following equations? 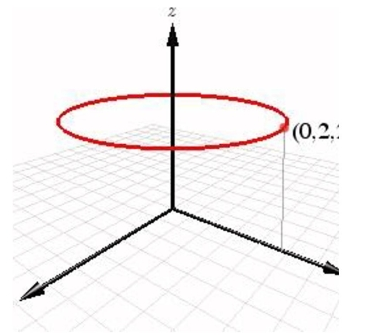
(Multiple Choice)
4.9/5  (27)
(27)
Showing 21 - 40 of 83
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)