Exam 14: Iterated Integrals and Area in the Plane
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Find the center of mass of the solid bounded by density function .
(Multiple Choice)
4.9/5  (32)
(32)
Find the center of mass of the rectangular lamina with vertices and for the density .
(Multiple Choice)
4.7/5  (34)
(34)
Evaluate the iterated integral below. Note that it is necessary to switch the order of integration.
(Multiple Choice)
4.8/5  (38)
(38)
Use a double integral to find the volume of the indicated solid. 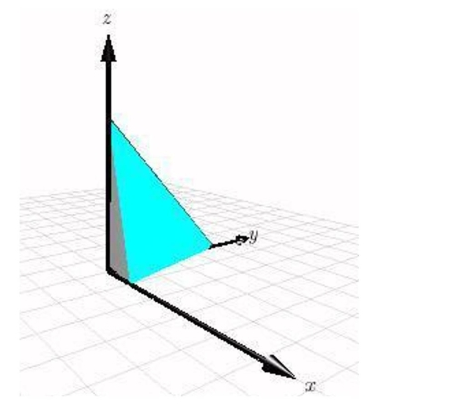
(Multiple Choice)
4.7/5  (35)
(35)
Find the mass of the lamina bounded by the graphs of the equations , and for the density
(Multiple Choice)
4.8/5  (43)
(43)
Set up a double integral that gives the area of the surface of the graph of f over the region R.
(Multiple Choice)
4.9/5  (35)
(35)
Set up and evaluate a double integral to find the volume of the solid bounded by the graphs of the equations and in the first octant.
(Multiple Choice)
4.8/5  (28)
(28)
Find the center of mass of the lamina bounded by the graphs of the equations and for the density
(Multiple Choice)
4.8/5  (29)
(29)
Find the area of the portion of the surface
that lies above the region . Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (26)
(26)
Use a double integral to find the volume of the indicated solid. 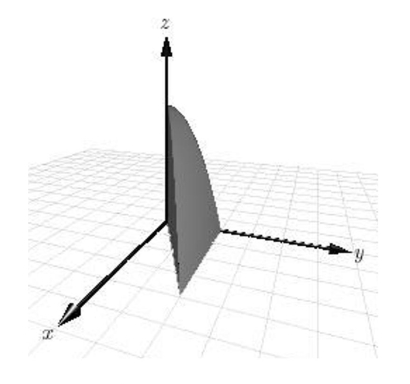
(Multiple Choice)
5.0/5  (31)
(31)
Set up a triple integral for the volume of the solid bounded by
(Multiple Choice)
4.9/5  (25)
(25)
Find the area of the surface for the portion of the sphere the cylinder
(Multiple Choice)
4.8/5  (35)
(35)
Use a double integral to find the volume of the indicated solid. 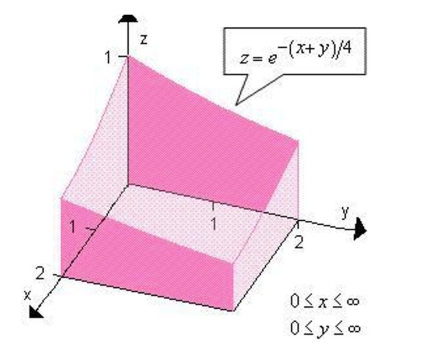
(Multiple Choice)
4.9/5  (34)
(34)
Use the indicated change of variables to evaluate the following double integral.
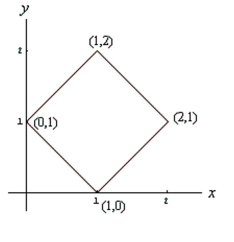
(Multiple Choice)
4.8/5  (30)
(30)
Use a change of variables to find the volume of the solid region lying below the surface and above the plane region : region bounded by the graphs of (Hint: Let .) Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (38)
(38)
Set up the double integral required to find the moment of inertia I, about the line , of the lamina bounded by the graphs of the equations and for the density . Use a computer algebra system to evaluate the double integral.
(Multiple Choice)
4.7/5  (27)
(27)
Set up and evaluate a double integral to find the volume of the solid bounded by the graphs of the equations
(Multiple Choice)
4.8/5  (29)
(29)
Showing 61 - 80 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)