Exam 14: Iterated Integrals and Area in the Plane
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Set up and evaluate a double integral to find the volume of the solid bounded by the graphs of the equations given below.
(Multiple Choice)
4.9/5  (41)
(41)
Use a change of variables to find the volume of the solid region lying below the surface and above the plane region : region bounded by the parallelogram with vertice . Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (38)
(38)
Find a such that the volume inside the hemisphere the cylinder is one-half the volume of the hemisphere. Round your answer to four decimal places.
(Multiple Choice)
4.8/5  (31)
(31)
Set up a double integral that gives the area of the surface on the graph of over the region
(Multiple Choice)
4.8/5  (31)
(31)
Use a double integral to find the area enclosed by the graph of 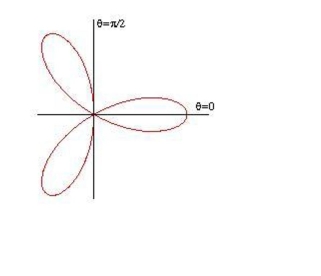
(Multiple Choice)
4.7/5  (30)
(30)
The area of a region R is given by the iterated integrals Switch the order of integration and show that both orders yield the same area. What is this area?
(Multiple Choice)
4.8/5  (41)
(41)
Use a double integral to find the volume of the indicated solid. 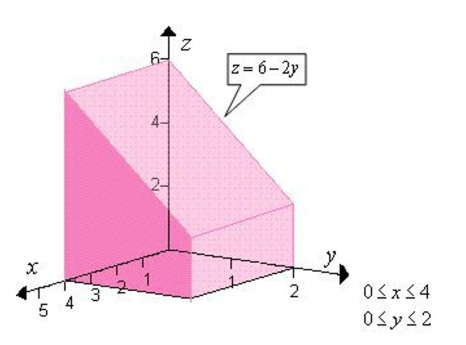
(Multiple Choice)
4.8/5  (29)
(29)
Set up a double integral that gives the area of the surface of the graph of f over the region R.
f(x,y)=-9xy+9 R=\{(x,y):-6\leqx\leq6,-8\leqy\leq8\}
(Multiple Choice)
4.9/5  (41)
(41)
Use spherical coordinates to find the z coordinate of the center of mass of the solid lying between two concentric hemispheres of radii 4 and 7, and having uniform density k.
(Multiple Choice)
4.7/5  (35)
(35)
Use cylindrical coordinates to find the volume of the solid inside the sphere and above the upper nappe of the cone .
(Multiple Choice)
4.8/5  (32)
(32)
Sketch the solid whose volume is given by the iterated integral given below and use the sketch to rewrite the integral using the indicated order of integration. Rewrite the integral using the order .
(Multiple Choice)
4.8/5  (32)
(32)
Find the center of mass of the rectangular lamina with vertices , and for the density
(Multiple Choice)
4.9/5  (40)
(40)
Find of the center of mass of the solid of given density by the graphs of the equations .
(Multiple Choice)
4.9/5  (38)
(38)
Find the area of the surface for the portion of the paraboloid in the first Octant.
(Multiple Choice)
4.7/5  (41)
(41)
Use an iterated integral to find the area of the region bounded by
(Multiple Choice)
5.0/5  (38)
(38)
A company produces a spherical object of radius 24 centimeters. A hole of radius 5 centimeters is drilled through the center of the object. Find the outer surface area of the object.
(Multiple Choice)
4.8/5  (37)
(37)
Find the mass of the lamina bounded by the graphs of the equations and for the density
(Multiple Choice)
4.9/5  (26)
(26)
Find the mass of the triangular lamina with vertices the density
(Multiple Choice)
4.8/5  (40)
(40)
Find the area of the surface given by : square with vertices
(Multiple Choice)
4.7/5  (40)
(40)
Showing 21 - 40 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)