Exam 14: Iterated Integrals and Area in the Plane
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Find the center of mass of the lamina bounded by the graphs of the equations , and for the density
(Multiple Choice)
4.7/5  (34)
(34)
A company produces a spherical object of radius 17 centimeters. A hole of radius 7 centimeters is drilled through the center of the object. Find the volume of the object.
(Multiple Choice)
4.9/5  (36)
(36)
Use a triple integral to find the volume of the solid bounded by the graphs of the equations
(Multiple Choice)
4.8/5  (40)
(40)
Find the area of the surface given by f(x,y)=xy R= (x,y):+\leq100
(Multiple Choice)
4.9/5  (32)
(32)
Use a double integral in polar coordinates to find the volume of the solid inside the hemisphere but outside the cylinder
(Multiple Choice)
4.9/5  (38)
(38)
Use a change of variables to find the volume of the solid region lying below the surface and above the plane region : region bounded by the square with vertices
(Multiple Choice)
4.8/5  (33)
(33)
over the region . Use a computer algebra system to evaluate the double integral. Round your answer to four decimal places.
(Multiple Choice)
4.8/5  (26)
(26)
Find the mass of the lamina described by the inequalities and , given that its density is . (Hint: Some of the integrals are simpler in polar coordinates.)
(Multiple Choice)
4.8/5  (38)
(38)
Determine the diameter of a hole that is drilled vertically through the center of the solid bounded by the graphs of the equations , and if one-tenth of the volume of the solid is removed. Round your answer to four decimal places.
(Multiple Choice)
4.8/5  (38)
(38)
Suppose the population density of a city is approximated by the model , where and are measured in miles. Integrate the density function over the indicated circular region to approximate the population of the city. Round your answer to the nearest integer.
(Multiple Choice)
4.8/5  (41)
(41)
Use an iterated integral to find the area of the region shown in the figure below.
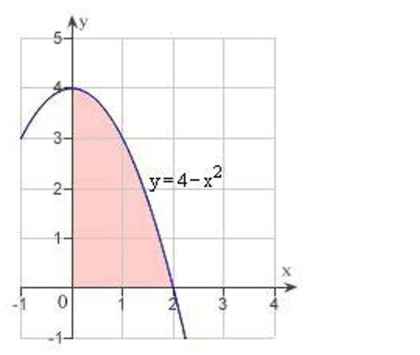
(Multiple Choice)
4.9/5  (32)
(32)
up a triple integral for the volume of the solid bounded above by the cylinder and below by the paraboloid .
(Multiple Choice)
4.9/5  (29)
(29)
Showing 81 - 100 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)