Exam 4: Circuit Theorems
Exam 1: Voltage, Current, Power, and Sources10 Questions
Exam 2: Circuit Laws10 Questions
Exam 3: Circuit Analysis Methods20 Questions
Exam 4: Circuit Theorems13 Questions
Exam 5: Operational Amplifier Circuits7 Questions
Exam 6: Capacitors and Inductors10 Questions
Exam 7: RL and RC Circuits14 Questions
Exam 8: RLC Circuits8 Questions
Exam 9: Phasors and Impedances8 Questions
Exam 10: Analysis of Phasor Transformed Circuits15 Questions
Exam 11: AC Power5 Questions
Exam 12: Three-Phase Systems6 Questions
Exam 13: Magnetically Coupled Circuits6 Questions
Exam 14: The Laplace Transform19 Questions
Exam 15: Circuits Analysis in the S-Domain26 Questions
Select questions type
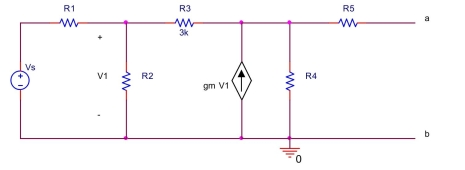
In the circuit shown below, let
Find the Norton equivalent current and the Norton equivalent resistance between terminals and .
Free
(Essay)
4.7/5  (42)
(42)
Correct Answer:
Finding open-circuit voltage:
clear all;
Vs ;
syms V1 V2
;
;
In-vpa
syms Va Vb
;
;
Answers:
the circuit shown below, 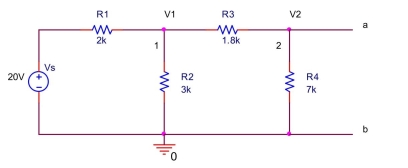 (a) Write a node equation at node 1 by summing the currents leaving node 1 .
(b) Write a node equation at node 2 by summing the currents leaving node 2 .
(c) Solve the node equations to find the Thévenin equivalent voltage between and , .
(d) Find the Thévenin equivalent resistance between and .
(a) Write a node equation at node 1 by summing the currents leaving node 1 .
(b) Write a node equation at node 2 by summing the currents leaving node 2 .
(c) Solve the node equations to find the Thévenin equivalent voltage between and , .
(d) Find the Thévenin equivalent resistance between and .
Free
(Essay)
4.9/5  (28)
(28)
Correct Answer:
clear all;
;
syms V1 V2
Answers:
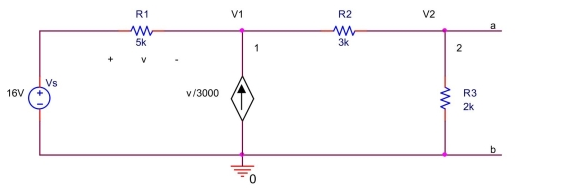
In the circuit shown below, (a) Write a node equation at node 1 by summing the currents away from node 1 .
(b) Write a node equation at node 2 by summing the currents away from node 2 .
(c) Solve the node equations to find the open circuit voltage .
(d) Find the short-circuit current and find the Norton resistance .
Free
(Essay)
5.0/5  (35)
(35)
Correct Answer:
Open circuit voltage: Short circuit current:
clear all;
;
syms
IVccs
Isum-I1+Ivces-I3
solve ( (Va-Vs)
ISc=Va/R2
Va-vpa
Isc=vpa
Answers:
In the circuit shown below, (a) Write a node equation at node 1 by summing the currents leaving node
(b) Write a node equation at node 2 by summing the currents leaving node 2 .
(c) Solve the node equations to find the Thévenin equivalent voltage between and , .
(d) Find the Thévenin equivalent resistance Ruth between and .
(e) Find the load resistance R. between and for the maximum power transfer to the load. Also, find the maximum power delivered to the load. 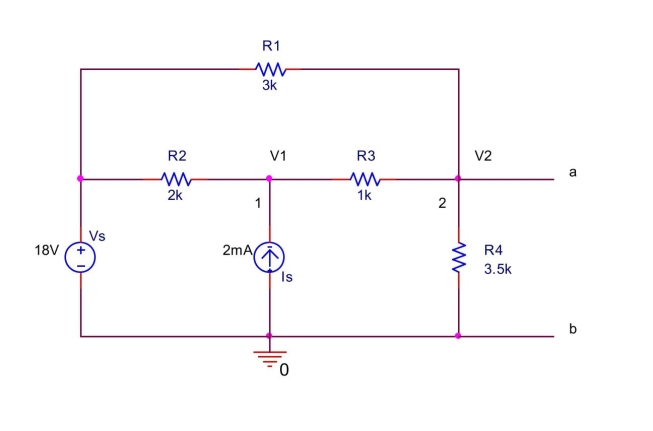
(Essay)
4.7/5  (33)
(33)
the circuit shown below, (a) Write a node equation at node 1 by summing the currents leaving node 1 .
(b) Write a node equation at node 2 by summing the currents leaving node 2 .
(c) Solve the two node equations to find at node
(d) Find the equivalent resistance seen from the terminals and looking into the circuit after deactivating the voltage source and the current source. 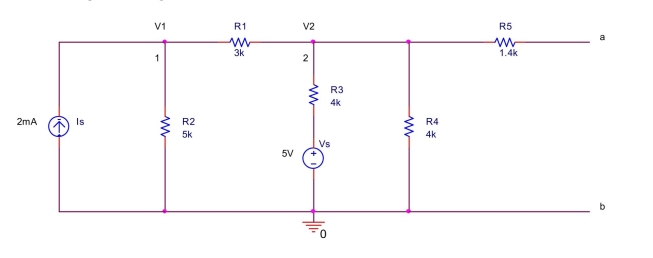
(Essay)
4.9/5  (28)
(28)
In the circuit shown below, let
Find the Norton equivalent current and the Norton equivalent resistance between terminals and . 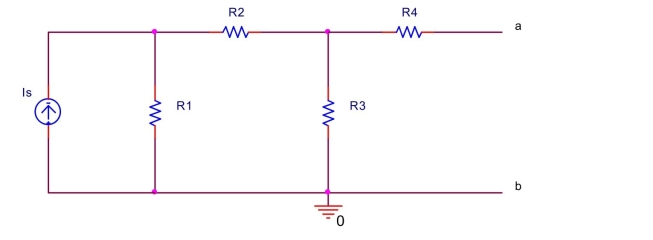
(Essay)
4.9/5  (35)
(35)
Find the Norton equivalent circuit across a and b for the circuit shown in Figure 2.
(a) Short circuit and by connecting a wire between and . Write a node equation at node 1 by summing the currents leaving node 1 . Solve the equation to find voltage .
(b) Find the short-circuit current between and , i.e., .
(c) Deactivate the current source and find the Norton equivalent resistance between and . 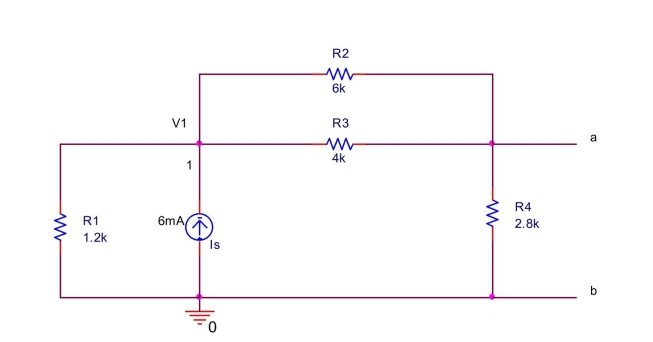
(Essay)
4.8/5  (37)
(37)
(a) Write a mesh equation for mesh 1 (left side) by summing the voltage drops around mesh 1 in a clockwise direction.
(b) Write a mesh equation for mesh 2 (right side) by summing the voltage drops around mesh 2 in a clockwise direction.
(c) Solve the mesh equations to find .
(d) Find the Thévenin equivalent voltage , which is the voltage across .
(e) Deactivate the voltage source and apply a test voltage of between and to find the Thévenin resistance .
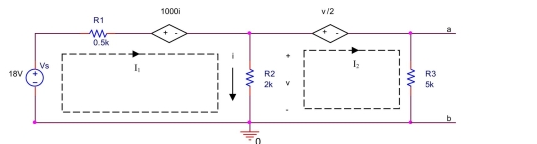
(Essay)
4.7/5  (37)
(37)
the circuit shown below, let
Find the Thévenin equivalent voltage and the Thévenin equivalent resistance Rth between terminals and .
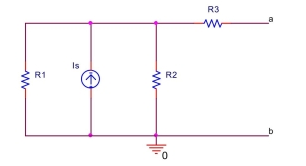
(Essay)
4.8/5  (33)
(33)
the circuit shown below, let
Find the Thévenin equivalent voltage and the Thévenin equivalent resistance between terminals and .
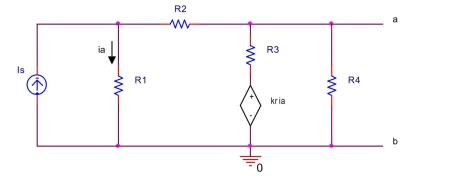
(Essay)
4.9/5  (44)
(44)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)