Exam 15: Section 8: Vector Analysis
Exam 1: Section 1: Preparation for Calculus16 Questions
Exam 1: Section 2: Preparation for Calculus26 Questions
Exam 1: Section 3: Preparation for Calculus23 Questions
Exam 1: Section 4: Preparation for Calculus16 Questions
Exam 1: Section 5: Preparation for Calculus25 Questions
Exam 1: Section 6: Preparation for Calculus8 Questions
Exam 2: Section 1: Limits and Their Properties10 Questions
Exam 2: Section 2: Limits and Their Properties14 Questions
Exam 2: Section 3: Limits and Their Properties25 Questions
Exam 2: Section 4: Limits and Their Properties20 Questions
Exam 2: Section 5 : Limits and Their Properties18 Questions
Exam 3: Section 1 : Differentiation20 Questions
Exam 3: Section 2: Differentiation25 Questions
Exam 3: Section 3: Differentiation26 Questions
Exam 3: Section 4 : Differentiation44 Questions
Exam 3: Section 5: Differentiation30 Questions
Exam 3: Section 6: Differentiation16 Questions
Exam 3: Section 7: Differentiation16 Questions
Exam 3: Section 8: Differentiation12 Questions
Exam 4: Section 1 : Applications of Differentiation19 Questions
Exam 4: Section 2: Applications of Differentiation17 Questions
Exam 4: Section 3: Applications of Differentiation17 Questions
Exam 4: Section 4: Applications of Differentiation26 Questions
Exam 4: Section 5: Applications of Differentiation23 Questions
Exam 4: Section 6: Applications of Differentiation22 Questions
Exam 4: Section 7: Applications of Differentiation15 Questions
Exam 4: Section 8: Applications of Differentiation16 Questions
Exam 4: Section 1: Integration19 Questions
Exam 4: Section 2: Integration17 Questions
Exam 4: Section 3: Integration19 Questions
Exam 4: Section 4: Integration18 Questions
Exam 4: Section 5: Integration31 Questions
Exam 4: Section 6: Integration18 Questions
Exam 4: Section 7: Integration27 Questions
Exam 4: Section 8: Integration16 Questions
Exam 4: Section 9: Integration20 Questions
Exam 6: Section 1: Differential Equations19 Questions
Exam 6: Section 2: Differential Equations25 Questions
Exam 6: Section 3: Differential Equations12 Questions
Exam 6: Section 4: Differential Equations14 Questions
Exam 6: Section 5: Differential Equations17 Questions
Exam 7: Section 1: Applications of Integration18 Questions
Exam 7: Section 2: Applications of Integration18 Questions
Exam 7: Section 3: Applications of Integration17 Questions
Exam 7: Section 4: Applications of Integration18 Questions
Exam 7: Section 5: Applications of Integration16 Questions
Exam 7: Section 6: Applications of Integration19 Questions
Exam 7: Section 7: Applications of Integration15 Questions
Exam 8: Section 1: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 2: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 3: Integration Techniques, Lhôpitals Rule, and Improper Integrals20 Questions
Exam 8: Section 4: Integration Techniques, Lhôpitals Rule, and Improper Integrals19 Questions
Exam 8: Section 5: Integration Techniques, Lhôpitals Rule, and Improper Integrals14 Questions
Exam 8: Section 6: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 7: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 8: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 9: Section 1: Infinite Series17 Questions
Exam 9: Section 2: Infinite Series23 Questions
Exam 9: Section 3: Infinite Series18 Questions
Exam 9: Section 4: Infinite Series21 Questions
Exam 9: Section 5: Infinite Series15 Questions
Exam 9: Section 6: Infinite Series21 Questions
Exam 9: Section 7: Infinite Series18 Questions
Exam 9: Section 8: Infinite Series18 Questions
Exam 9: Section 9: Infinite Series19 Questions
Exam 9: Section 10: Infinite Series16 Questions
Exam 10: Section 1: Conics, Parametric Equations, and Polar Coordinates26 Questions
Exam 10: Section 2: Conics, Parametric Equations, and Polar Coordinates17 Questions
Exam 10: Section 3: Conics, Parametric Equations, and Polar Coordinates22 Questions
Exam 10: Section 4: Conics, Parametric Equations, and Polar Coordinates15 Questions
Exam 10: Section 5: Conics, Parametric Equations, and Polar Coordinates18 Questions
Exam 10: Section 6: Conics, Parametric Equations, and Polar Coordinates19 Questions
Exam 11: Section 1: Vectors and the Geometry of Space20 Questions
Exam 11: Section 2: Vectors and the Geometry of Space21 Questions
Exam 11: Section 3: Vectors and the Geometry of Space18 Questions
Exam 11: Section 4: Vectors and the Geometry of Space18 Questions
Exam 11: Section 5: Vectors and the Geometry of Space21 Questions
Exam 11: Section 6: Vectors and the Geometry of Space20 Questions
Exam 11: Section 7: Vectors and the Geometry of Space19 Questions
Exam 12: Section 1: Vector-Valued Functions21 Questions
Exam 12: Section 2: Vector-Valued Functions24 Questions
Exam 12: Section 3: Vector-Valued Functions18 Questions
Exam 12: Section 4: Vector-Valued Functions20 Questions
Exam 12: Section 5: Vector-Valued Functions19 Questions
Exam 13: Section 1: Functions of Several Variables19 Questions
Exam 13: Section 2: Functions of Several Variables22 Questions
Exam 13: Section 3: Functions of Several Variables23 Questions
Exam 13: Section 4: Functions of Several Variables17 Questions
Exam 13: Section 6: Functions of Several Variables20 Questions
Exam 13: Section 7: Functions of Several Variables20 Questions
Exam 13: Section 8: Functions of Several Variables20 Questions
Exam 13: Section 9: Functions of Several Variables17 Questions
Exam 13: Section 10: Functions of Several Variables18 Questions
Exam 14: Section 1: Multiple Integration20 Questions
Exam 14: Section 2: Multiple Integration19 Questions
Exam 14: Section 3: Multiple Integration20 Questions
Exam 14: Section 4: Multiple Integration18 Questions
Exam 14: Section 5: Multiple Integration18 Questions
Exam 14: Section 6: Multiple Integration19 Questions
Exam 14: Section 7: Multiple Integration19 Questions
Exam 14: Section 8: Multiple Integration19 Questions
Exam 15: Section 1: Vector Analysis21 Questions
Exam 15: Section 2: Vector Analysis18 Questions
Exam 15: Section 3: Vector Analysis18 Questions
Exam 15: Section 4: Vector Analysis18 Questions
Exam 15: Section 5: Vector Analysis21 Questions
Exam 15: Section 6: Vector Analysis18 Questions
Exam 15: Section 7: Vector Analysis18 Questions
Exam 15: Section 8: Vector Analysis17 Questions
Select questions type
Let 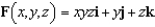 and let S be the plane
and let S be the plane 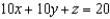 in the first octant. Verify Stokes's Theorem by evaluating
in the first octant. Verify Stokes's Theorem by evaluating 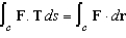 as a line integral and as a double integral.
as a line integral and as a double integral.
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
D
Use Stokes's Theorem to evaluate 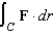 where
where 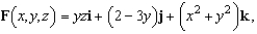
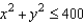 and S is the first-octant portion of
and S is the first-octant portion of 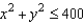 over
over 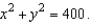 Use a computer algebra system to verify your result.
Use a computer algebra system to verify your result.
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
C
Use Stokes's Theorem to evaluate 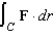 where
where 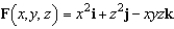 and S is
and S is 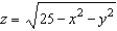 .Use a computer algebra system to verify your result.
.Use a computer algebra system to verify your result.
Free
(Multiple Choice)
4.7/5  (30)
(30)
Correct Answer:
E
Use Stokes's Theorem to evaluate 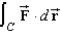 .Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above.
.Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above. 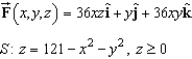
(Multiple Choice)
4.8/5  (34)
(34)
Use Stokes's Theorem to evaluate 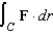 where
where 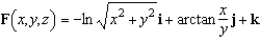 and S is
and S is 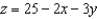 over
over 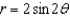 in the first octant. Use a computer algebra system to verify your result.
in the first octant. Use a computer algebra system to verify your result.
(Multiple Choice)
4.7/5  (33)
(33)
Use Stokes's Theorem to evaluate 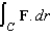 where
where 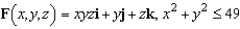 and S is the first-octant portion of
and S is the first-octant portion of 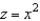 over
over 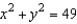 . Use a computer algebra system to verify your result.
. Use a computer algebra system to verify your result.
(Multiple Choice)
4.8/5  (29)
(29)
Let 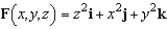 and let S be the graph of
and let S be the graph of 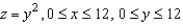 . Verify Stokes's Theorem by evaluating
. Verify Stokes's Theorem by evaluating 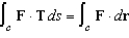 as a line integral and as a double integral.
as a line integral and as a double integral.
(Multiple Choice)
4.9/5  (41)
(41)
The motion of a liquid in a cylindrical container of radius 1 is described by the velocity field 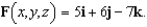 Find
Find 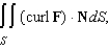 where S is the upper surface of the cylindrical container.
where S is the upper surface of the cylindrical container.
(Multiple Choice)
4.7/5  (35)
(35)
The motion of a liquid in a cylindrical container of radius 1 is described by the velocity field 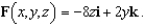 Find
Find 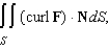 where S is the upper surface of the cylindrical container.
where S is the upper surface of the cylindrical container.
(Multiple Choice)
4.9/5  (35)
(35)
Use Stokes's Theorem to evaluate 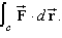 Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above.
Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above. 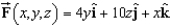 C: triangle with vertices
C: triangle with vertices 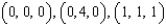
(Multiple Choice)
4.8/5  (31)
(31)
Verify Stokes's Theorem by evaluating 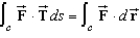 as a line integral and as a double integral .
as a line integral and as a double integral . 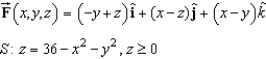
(Multiple Choice)
4.9/5  (29)
(29)
Let 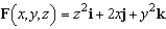 and let S be the graph of
and let S be the graph of 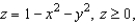 oriented counterclockwise. Use Stokes's Theorem to evaluate
oriented counterclockwise. Use Stokes's Theorem to evaluate 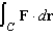 .
.
(Multiple Choice)
4.8/5  (39)
(39)
Use Stokes's Theorem to evaluate 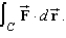 Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above.
Use a computer algebra system to verify your results. Note: C is oriented counterclockwise as viewed from above. 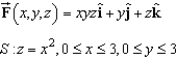
(Multiple Choice)
4.7/5  (34)
(34)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)