Explore all topics
Start Free Trial
Need Help? Contact us
back arrowfull exam logo
search
ai logoChat with AI
Servicesarrow
Discoverarrow

Topics

Explore all topics
Discover more topics

Exam 14: Section 1: Multiple Integration

arrow
Exam 1: Section 1: Preparation for Calculus16 Questionsadd course
Exam 1: Section 2: Preparation for Calculus26 Questionsadd course
Exam 1: Section 3: Preparation for Calculus23 Questionsadd course
Exam 1: Section 4: Preparation for Calculus16 Questionsadd course
Exam 1: Section 5: Preparation for Calculus25 Questionsadd course
Exam 1: Section 6: Preparation for Calculus8 Questionsadd course
Exam 2: Section 1: Limits and Their Properties10 Questionsadd course
Exam 2: Section 2: Limits and Their Properties14 Questionsadd course
Exam 2: Section 3: Limits and Their Properties25 Questionsadd course
Exam 2: Section 4: Limits and Their Properties20 Questionsadd course
Exam 2: Section 5 : Limits and Their Properties18 Questionsadd course
Exam 3: Section 1 : Differentiation20 Questionsadd course
Exam 3: Section 2: Differentiation25 Questionsadd course
Exam 3: Section 3: Differentiation26 Questionsadd course
Exam 3: Section 4 : Differentiation44 Questionsadd course
Exam 3: Section 5: Differentiation30 Questionsadd course
Exam 3: Section 6: Differentiation16 Questionsadd course
Exam 3: Section 7: Differentiation16 Questionsadd course
Exam 3: Section 8: Differentiation12 Questionsadd course
Exam 4: Section 1 : Applications of Differentiation19 Questionsadd course
Exam 4: Section 2: Applications of Differentiation17 Questionsadd course
Exam 4: Section 3: Applications of Differentiation17 Questionsadd course
Exam 4: Section 4: Applications of Differentiation26 Questionsadd course
Exam 4: Section 5: Applications of Differentiation23 Questionsadd course
Exam 4: Section 6: Applications of Differentiation22 Questionsadd course
Exam 4: Section 7: Applications of Differentiation15 Questionsadd course
Exam 4: Section 8: Applications of Differentiation16 Questionsadd course
Exam 4: Section 1: Integration19 Questionsadd course
Exam 4: Section 2: Integration17 Questionsadd course
Exam 4: Section 3: Integration19 Questionsadd course
Exam 4: Section 4: Integration18 Questionsadd course
Exam 4: Section 5: Integration31 Questionsadd course
Exam 4: Section 6: Integration18 Questionsadd course
Exam 4: Section 7: Integration27 Questionsadd course
Exam 4: Section 8: Integration16 Questionsadd course
Exam 4: Section 9: Integration20 Questionsadd course
Exam 6: Section 1: Differential Equations19 Questionsadd course
Exam 6: Section 2: Differential Equations25 Questionsadd course
Exam 6: Section 3: Differential Equations12 Questionsadd course
Exam 6: Section 4: Differential Equations14 Questionsadd course
Exam 6: Section 5: Differential Equations17 Questionsadd course
Exam 7: Section 1: Applications of Integration18 Questionsadd course
Exam 7: Section 2: Applications of Integration18 Questionsadd course
Exam 7: Section 3: Applications of Integration17 Questionsadd course
Exam 7: Section 4: Applications of Integration18 Questionsadd course
Exam 7: Section 5: Applications of Integration16 Questionsadd course
Exam 7: Section 6: Applications of Integration19 Questionsadd course
Exam 7: Section 7: Applications of Integration15 Questionsadd course
Exam 8: Section 1: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questionsadd course
Exam 8: Section 2: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questionsadd course
Exam 8: Section 3: Integration Techniques, Lhôpitals Rule, and Improper Integrals20 Questionsadd course
Exam 8: Section 4: Integration Techniques, Lhôpitals Rule, and Improper Integrals19 Questionsadd course
Exam 8: Section 5: Integration Techniques, Lhôpitals Rule, and Improper Integrals14 Questionsadd course
Exam 8: Section 6: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questionsadd course
Exam 8: Section 7: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questionsadd course
Exam 8: Section 8: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questionsadd course
Exam 9: Section 1: Infinite Series17 Questionsadd course
Exam 9: Section 2: Infinite Series23 Questionsadd course
Exam 9: Section 3: Infinite Series18 Questionsadd course
Exam 9: Section 4: Infinite Series21 Questionsadd course
Exam 9: Section 5: Infinite Series15 Questionsadd course
Exam 9: Section 6: Infinite Series21 Questionsadd course
Exam 9: Section 7: Infinite Series18 Questionsadd course
Exam 9: Section 8: Infinite Series18 Questionsadd course
Exam 9: Section 9: Infinite Series19 Questionsadd course
Exam 9: Section 10: Infinite Series16 Questionsadd course
Exam 10: Section 1: Conics, Parametric Equations, and Polar Coordinates26 Questionsadd course
Exam 10: Section 2: Conics, Parametric Equations, and Polar Coordinates17 Questionsadd course
Exam 10: Section 3: Conics, Parametric Equations, and Polar Coordinates22 Questionsadd course
Exam 10: Section 4: Conics, Parametric Equations, and Polar Coordinates15 Questionsadd course
Exam 10: Section 5: Conics, Parametric Equations, and Polar Coordinates18 Questionsadd course
Exam 10: Section 6: Conics, Parametric Equations, and Polar Coordinates19 Questionsadd course
Exam 11: Section 1: Vectors and the Geometry of Space20 Questionsadd course
Exam 11: Section 2: Vectors and the Geometry of Space21 Questionsadd course
Exam 11: Section 3: Vectors and the Geometry of Space18 Questionsadd course
Exam 11: Section 4: Vectors and the Geometry of Space18 Questionsadd course
Exam 11: Section 5: Vectors and the Geometry of Space21 Questionsadd course
Exam 11: Section 6: Vectors and the Geometry of Space20 Questionsadd course
Exam 11: Section 7: Vectors and the Geometry of Space19 Questionsadd course
Exam 12: Section 1: Vector-Valued Functions21 Questionsadd course
Exam 12: Section 2: Vector-Valued Functions24 Questionsadd course
Exam 12: Section 3: Vector-Valued Functions18 Questionsadd course
Exam 12: Section 4: Vector-Valued Functions20 Questionsadd course
Exam 12: Section 5: Vector-Valued Functions19 Questionsadd course
Exam 13: Section 1: Functions of Several Variables19 Questionsadd course
Exam 13: Section 2: Functions of Several Variables22 Questionsadd course
Exam 13: Section 3: Functions of Several Variables23 Questionsadd course
Exam 13: Section 4: Functions of Several Variables17 Questionsadd course
Exam 13: Section 6: Functions of Several Variables20 Questionsadd course
Exam 13: Section 7: Functions of Several Variables20 Questionsadd course
Exam 13: Section 8: Functions of Several Variables20 Questionsadd course
Exam 13: Section 9: Functions of Several Variables17 Questionsadd course
Exam 13: Section 10: Functions of Several Variables18 Questionsadd course
Exam 14: Section 1: Multiple Integration20 Questionsadd course
Exam 14: Section 2: Multiple Integration19 Questionsadd course
Exam 14: Section 3: Multiple Integration20 Questionsadd course
Exam 14: Section 4: Multiple Integration18 Questionsadd course
Exam 14: Section 5: Multiple Integration18 Questionsadd course
Exam 14: Section 6: Multiple Integration19 Questionsadd course
Exam 14: Section 7: Multiple Integration19 Questionsadd course
Exam 14: Section 8: Multiple Integration19 Questionsadd course
Exam 15: Section 1: Vector Analysis21 Questionsadd course
Exam 15: Section 2: Vector Analysis18 Questionsadd course
Exam 15: Section 3: Vector Analysis18 Questionsadd course
Exam 15: Section 4: Vector Analysis18 Questionsadd course
Exam 15: Section 5: Vector Analysis21 Questionsadd course
Exam 15: Section 6: Vector Analysis18 Questionsadd course
Exam 15: Section 7: Vector Analysis18 Questionsadd course
Exam 15: Section 8: Vector Analysis17 Questionsadd course
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags
search iconSearch Question
flashcardsStudy Flashcards
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags

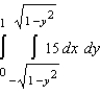The area of a region R is given by the iterated integral The area of a region R is given by the iterated integral . Switch the order of integration and show that both orders yield the same area. What is this area? . Switch the order of integration and show that both orders yield the same area. What is this area?

Free
(Multiple Choice)
4.8/5
(29)
Question 1
Correct Answer:
Verified

C

Evaluate the following integral. Evaluate the following integral.

Free
(Multiple Choice)
4.8/5
(36)
Question 2
Correct Answer:
Verified

D

Evaluate the iterated integral below. Note that it is necessary to switch the order of integration. Evaluate the iterated integral below. Note that it is necessary to switch the order of integration.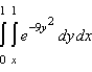

Free
(Multiple Choice)
4.8/5
(41)
Question 3
Correct Answer:
Verified

B

Evaluate the following iterated integral. Evaluate the following iterated integral.

(Multiple Choice)
4.8/5
(38)
Question 4

Evaluate the iterated integral Evaluate the iterated integral 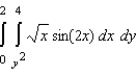by switching the order of integration. Round your answer to three decimal places. by switching the order of integration. Round your answer to three decimal places.

(Multiple Choice)
4.7/5
(34)
Question 5

The area of a region R is given by the iterated integrals The area of a region R is given by the iterated integrals 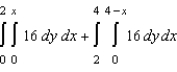. Switch the order of integration and show that both orders yield the same area. What is this area? . Switch the order of integration and show that both orders yield the same area. What is this area?

(Multiple Choice)
4.9/5
(32)
Question 6

Use an iterated integral to find the area of the region shown in the figure below. Use an iterated integral to find the area of the region shown in the figure below.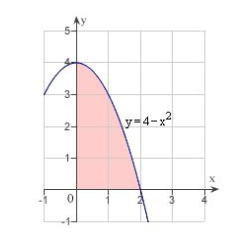

(Multiple Choice)
4.9/5
(18)
Question 7

Evaluate the following integral. Evaluate the following integral.

(Multiple Choice)
4.9/5
(41)
Question 8

Evaluate the following improper integral. Evaluate the following improper integral.

(Multiple Choice)
5.0/5
(45)
Question 9

Sketch the region R and evaluate the iterated integral. Sketch the region R and evaluate the iterated integral.

(Multiple Choice)
4.9/5
(26)
Question 10

Use an iterated integral to find the area of the region bounded by Use an iterated integral to find the area of the region bounded by . .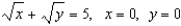

(Multiple Choice)
5.0/5
(28)
Question 11

Evaluate the following integral. Evaluate the following integral.

(Multiple Choice)
4.8/5
(26)
Question 12

Evaluate the following iterated integral. Evaluate the following iterated integral.

(Multiple Choice)
4.7/5
(36)
Question 13

Use an iterated integral to find the area of the region bounded by Use an iterated integral to find the area of the region bounded by . .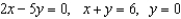

(Multiple Choice)
4.9/5
(43)
Question 14

Evaluate the following iterated integral. Evaluate the following iterated integral.

(Multiple Choice)
4.8/5
(33)
Question 15

Evaluate the improper iterated integral Evaluate the improper iterated integral . .

(Multiple Choice)
4.8/5
(26)
Question 16

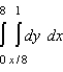The area of a region R is given by the iterated integral The area of a region R is given by the iterated integral . Switch the order of integration and show that both orders yield the same area. What is this area? . Switch the order of integration and show that both orders yield the same area. What is this area?

(Multiple Choice)
4.9/5
(35)
Question 17

Sketch the region R of integration and then switch the order of integration for the following integral. Sketch the region R of integration and then switch the order of integration for the following integral.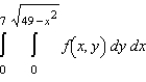

(Multiple Choice)
4.7/5
(32)
Question 18

Evaluate the following iterated integral. Evaluate the following iterated integral.

(Multiple Choice)
4.7/5
(36)
Question 19

Use an iterated integral to find the area of the region bounded by the graphs of the equations Use an iterated integral to find the area of the region bounded by the graphs of the equations 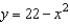and . and Use an iterated integral to find the area of the region bounded by the graphs of the equations and . .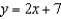

(Multiple Choice)
4.8/5
(25)
Question 20
close modal

Filters

  • Essay(0)
  • Multiple Choice(0)
  • Short Answer(0)
  • True False(0)
  • Matching(0)