Exam 9: Vectors and the Geometry of Space
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
Describe the surface whose equation in cylindrical coordinates is = 3.
(Multiple Choice)
4.7/5  (36)
(36)
Find an equation of a plane containing the point P(2, -1, 1) and the z-axis.
(Multiple Choice)
5.0/5  (36)
(36)
Let f(x, y) = (a) Evaluate .(b) Find the domain of f.(c) Find the range of f.
(Essay)
4.9/5  (37)
(37)
Let f(x, y) = (a) Evaluate .(b) Find the domain of f.(c) Find the range of f.
(Essay)
4.9/5  (28)
(28)
Do the two lines and intersect? If so, find the point of intersection.
(Essay)
4.7/5  (32)
(32)
Let a be the vector shown below. Find the horizontal component b and the vertical component c of a if a = 3. 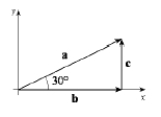
(Essay)
4.9/5  (43)
(43)
Find the volume of the parallelepiped spanned by the vectors 2i + 3j + 5k, 3i - j + 4k, and -i - 2j + 3k.
(Short Answer)
4.8/5  (43)
(43)
Find the coordinate of the terminal point of a vector whose initial point is .
(Multiple Choice)
4.7/5  (25)
(25)
Let a and b be vectors such that = 2 and = 3. Assume that the angle between a and b is . Find .
(Short Answer)
5.0/5  (26)
(26)
Find the area of quadrilateral ABCD. Note that ABCD is not a parallelogram. 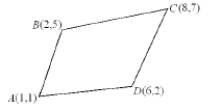
(Short Answer)
5.0/5  (30)
(30)
Find the coordinate of the terminal point of a vector whose initial point is .
(Multiple Choice)
4.9/5  (43)
(43)
Showing 181 - 200 of 269
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)